监督学习(supervised learning)
给定一个input x,给出x的正确答案,即标签 y。机器通过这些大量的例子训练学习后使得遇到一个崭新的x时,能够辨别出x对应的y是多少
专业术语:
training set:训练集x x x y y y ( x , y ) (x,y) ( x , y ) ( x i , y i ) (x^{i},y^{i}) ( x i , y i ) i t h i^{th} i t h m m m
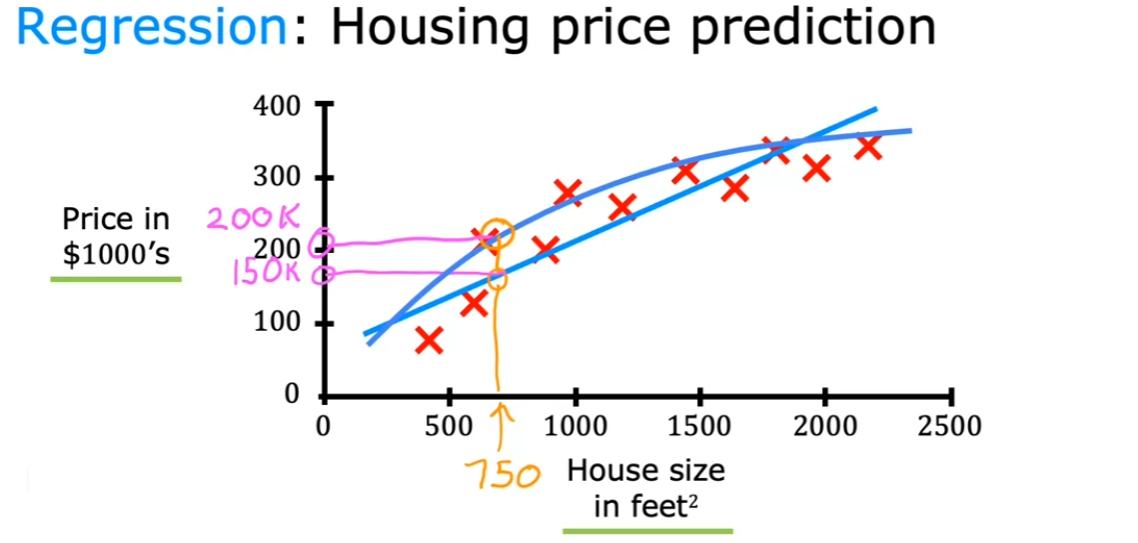
回归问题(Regression)
给定x,预测x对应的数字y(y的取值为无穷)
一元线性回归
f ( x ) = w x + b f(x)=wx+b f ( x ) = w x + b w . b w.b w . b
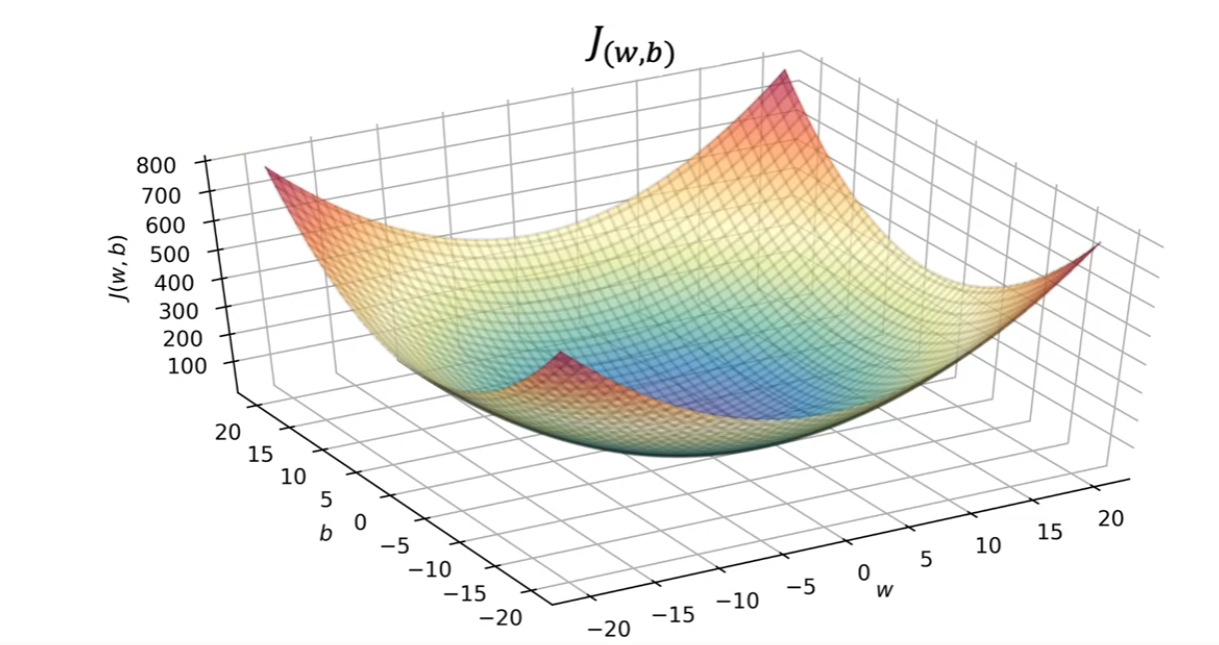
损失函数 :J ( w , b ) = 1 2 m ∑ 1 m ( y ^ − y ) 2 J(w,b)= \frac{1}{2m} \sum _{1}^{m} (\hat{y}-y)^{2} J ( w , b ) = 2 m 1 ∑ 1 m ( y ^ − y ) 2
g o a l : m i n i z e ( J ( w , b ) ) goal:minize(J(w,b)) g o a l : mini ze ( J ( w , b ))
梯度下降法
前置知识
首先需要复习一下方向导数和梯度的概念:方向导数 :若函数z = f ( x , y ) z=f(x,y) z = f ( x , y ) P ( x , y ) P(x,y) P ( x , y )
α z α l ∣ ( x , y ) = lim ρ → 0 Δ z Δ 自变量 = lim ρ → 0 f ( x + Δ x , y + Δ y ) − f ( x , y ) x 2 + y 2 ( ρ = x 2 + y 2 ) \frac{\alpha z}{\alpha l} |_{(x,y)} = \lim_{\rho \to 0} \frac{\Delta z}{\Delta 自变量}= \lim_{\rho \to 0} \frac{f(x+\Delta x,y+\Delta y)-f(x,y)}{\sqrt{x^{2}+y^{2}}} (\rho =\sqrt{x^{2}+y^{2}})
α l α z ∣ ( x , y ) = ρ → 0 lim Δ 自变量 Δ z = ρ → 0 lim x 2 + y 2 f ( x + Δ x , y + Δ y ) − f ( x , y ) ( ρ = x 2 + y 2 )
特别地,当z = f ( x , y ) z=f(x,y) z = f ( x , y ) P ( x , y ) P(x,y) P ( x , y ) z = f ( x , y ) z=f(x,y) z = f ( x , y )
α z α l ∣ ( x , y ) = α z α x c o s α + α z α y c o s β = { α z α x , α z α y } ⋅ { c o s α , c o s β } \frac{\alpha z}{\alpha l} |_{(x,y)} = \frac{\alpha z}{\alpha x}cos{\alpha}+\frac{\alpha z}{\alpha y}cos{\beta} =\{\frac{\alpha z}{\alpha x},\frac{\alpha z}{\alpha y} \}\cdot \{cos{\alpha},cos{\beta}\}
α l α z ∣ ( x , y ) = αx α z cos α + α y α z cos β = { αx α z , α y α z } ⋅ { cos α , cos β }
故当方向l ⃗ = { c o s α , c o s β } \vec {l}=\{cos{\alpha},cos{\beta}\} l = { cos α , cos β } { α z α x , α z α y } \{\frac{\alpha z}{\alpha x},\frac{\alpha z}{\alpha y}\} { αx α z , α y α z } 梯度 :g a r d f = { α z α x , α z α y } gard f=\{\frac{\alpha z}{\alpha x},\frac{\alpha z}{\alpha y} \} g a r df = { αx α z , α y α z }
算法描述
梯度下降法即每次迭代,都使得( J ( w , b ) ) (J(w,b)) ( J ( w , b )) w = w − α ⋅ α J α w = w − α ⋅ 1 m ∑ 1 m ( f w , b ( x i ) − y i ) x i w=w-\alpha \cdot \frac{\alpha J}{\alpha w}=w-\alpha \cdot \frac{1}{m}\sum_{1}^{m}(f_{w,b}(x_{i})-y_{i})x_{i} w = w − α ⋅ α w α J = w − α ⋅ m 1 ∑ 1 m ( f w , b ( x i ) − y i ) x i b = b − α ⋅ α J α b = b − α ⋅ 1 m ∑ 1 m ( f w , b ( x i ) − y i ) b=b-\alpha \cdot \frac{\alpha J}{\alpha b}=b-\alpha \cdot \frac{1}{m}\sum_{1}^{m}(f_{w,b}(x_{i})-y_{i}) b = b − α ⋅ α b α J = b − α ⋅ m 1 ∑ 1 m ( f w , b ( x i ) − y i ) α \alpha α ∈ ( 0 , 1 ) \in (0,1) ∈ ( 0 , 1 )
如果α \alpha α
如果α \alpha α
但对于固定的学习率来讲梯度下降法得到的函数最小值和初值有关,每次得到是初值附近的局部最优解 然而对于一元线性回归来讲,其损失函数是一个凹函数(convex function),其极小值点只有一个,故梯度下降法在此适用
分类问题(Classfication)
给定x,预测x对应的类别y(取值范围为种类数)
无监督学习(unsupervised learning)
find things in unlabled data
the data comes only with inputs x but not output labels y, and the algorithm has to find some structure or some pattern or something interesting in the data
聚类问题
异常检测
降维