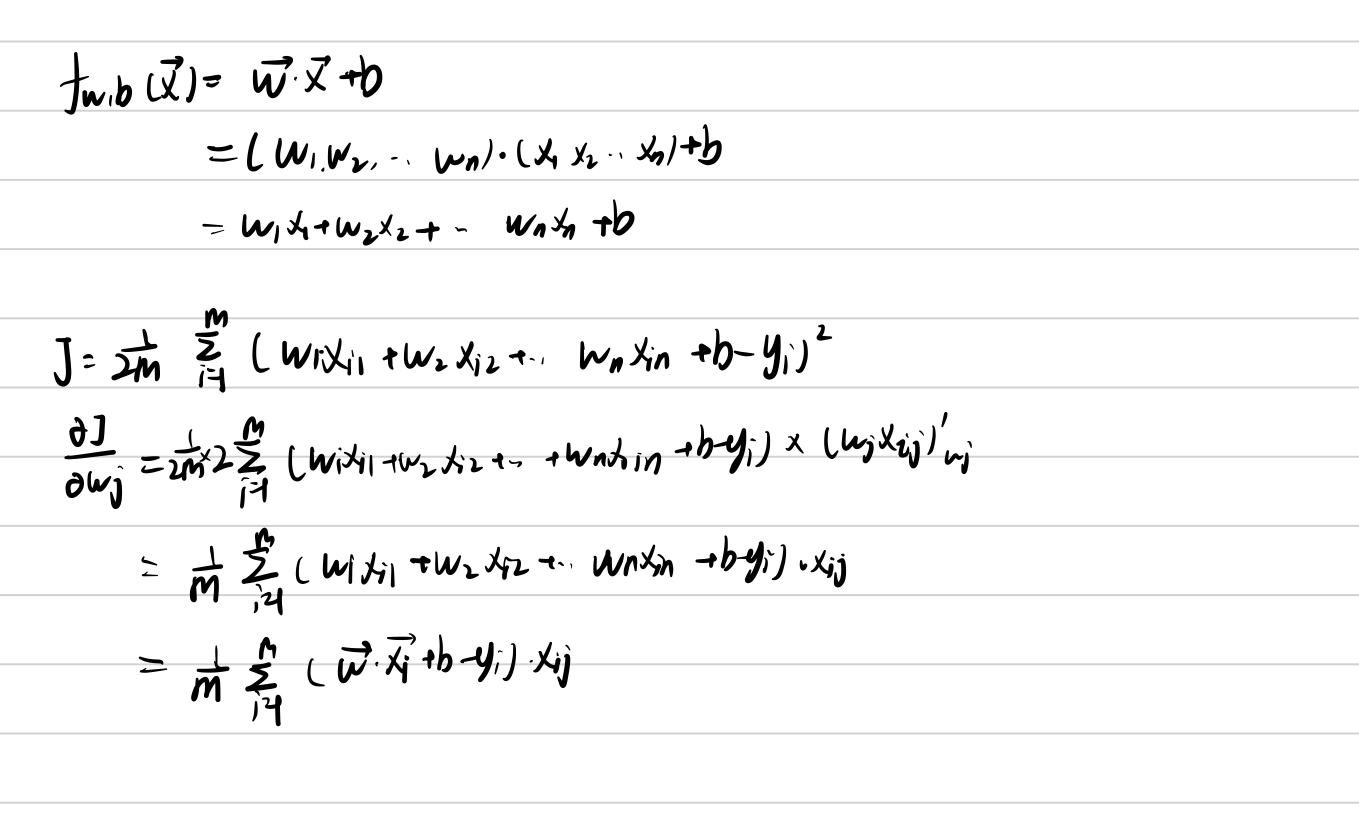Machine Learning 2 多元线性回归

多元线性回归

概述

特征：

• 多个输入特征

拟合方程：$f(\vec x)= \vec w \cdot \vec x+b$

其中$\vec w=[w_{1},w_{2},w_{3}...w_{n}],\vec x =[x_{1},x_{2}....x_{n}]$

$w_{j}=w_{j}-\alpha \cdot \frac{\alpha J}{\alpha w_{j}}=w_{j}-\alpha \cdot \frac{1}{m}\sum_{i=1}^{m}(f_{w,b}(x_{i})-y_{i})x_{ij}$ 其中$j=1,2…n,i=1,2…m $

$b=b-\alpha \cdot \frac{\alpha J}{\alpha b}=b-\alpha \cdot \frac{1}{m}\sum_{1}^{m}(f_{w,b}(x_{i})-y_{i})$

$m$是数据的组数，$n$是一组数据的维度

推导：

梯度下降法分类

批梯度下降（batch gradient descent）

计算出所有样本的误差之和再更新参数

$w_{j}=w_{j}-\sum_{i=1}^{m}(f(x)-y^{(i)})x_{j}^{(i)}$

• 保证一定可以收敛到损失函数的全局最优

随机梯度下降（stochastic gradient descent）

计算出一个样本的误差就更新参数

$for\space i=1\space to \space m:$

$\space w_{j}=w_{j}-(f(x)-y^{(i)})x_{j}^{(i)}$

• 这种算法不一定保证能够收敛到损失函数的全局最优，但实践得出大部分情况下所得答案都和全局最优解近似
• 计算速度比批梯度下降法快，适用于数据量比较大的情况

梯度下降优化方法

特征压缩

思想：

• 注意到梯度下降法中每次迭代$w_{j}=w_{j}-\alpha \cdot \frac{1}{m}\sum_{i=1}^{m}(f_{w,b}(x_{i})-y_{i})x_{ij}$
• 其中$w_{j_{1}},w_{j_{2}}$更新速度因$x_{ij}$的不同而不同，导致两个参数更新速度可能存在较大差异，难以同时收敛
• 故考虑将每个特征的范围都压缩到范围基本一致的区间内

具体压缩方法：

• Mean normalization：

$$\begin{align} x_i :&= \dfrac{x_i - \mu_i}{max - min} \end{align}$$

• Z-score normalization:

$$\begin{align} x^{(i)}_j &= \dfrac{x^{(i)}_j - \mu_j}{\sigma_j}\\ \mu_j &= \frac{1}{m} \sum_{i=0}^{m-1} x^{(i)}_j \\ \sigma^2_j &= \frac{1}{m} \sum_{i=0}^{m-1} (x^{(i)}_j - \mu_j)^2 \\ \end{align}$$

特征工程（当出现高次项即为多项式回归）

思想：

• 利用已有的特征组合推出新的特征加入到拟合方程中
• 例如已知房屋的长和宽，来预测价格。相比于$f(x)=w_{1}*x_{1}+w_{2}*x_{2}$,不妨设$x_{3}=x_{1}*x_{2}$ 表示面积，直觉上面积和价格上存在更强的关系，故$f(x)=w_{1}*x_{1}+w_{2}*x_{2}+w_{3}*x_{3}$效果更好。

Numpy

• 矩阵乘法：X@W

• 对应元素相乘：X*W

• 广播规则

X=[[1,2],[3,4]],w=[1,2]

X@w=$[1*1+2*2,3*1+4*2]=[5,11]$

X*w（触发广播规则，w作用在X的每一行上）=[[1,4],[3,8]]

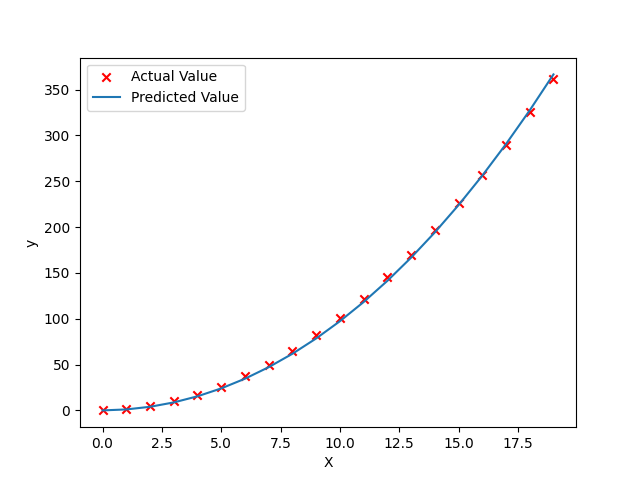
代码实现：

import numpy as np
import matplotlib.pyplot as plt
def run_gradient(X,y,iter,alpha):
    m = X.shape[0] #数据的组数
    n = X.shape[1] #特征维度
    J = 0
    w = np.zeros(n)
    b =0
    J_history=[]
    for k in range(iter):
        #cont for dw and db
        for j in range(n):
            dw =0
            for i in range(m):
                dw = dw +(np.dot(w,X[i,:])+b-y[i])*X[i,j]
            dw/=m
            w[j] = w[j] -alpha*dw
        db = 0
        for i in range(m):
            db = db +(np.dot(w,X[i,:])+b-y[i])
        db/=m
        b = b -alpha*db
        # cont for costfunction
        for i in range(m):
            J = J +(np.dot(w,X[i])+b - y[i])**2
        J=J/(2*m)
        J_history.append(J)
    return w,b,J_history

x = np.arange(0,20,1)
X = x.reshape(-1,1)
X = np.c_[x, x**2, x**3]  #Feature Engineering  
y = 1 + x**2
w,b,J_his= run_gradient(X,y,30000,1e-7)
print(w)
print(b)
plt.scatter(x,y,marker='x',c='r',label='Actual Value')
plt.plot(x,X@w+b,label="Predicted Value")
plt.xlabel("X"); plt.ylabel("y"); plt.legend(); plt.show()

注意事项：

• 由于代码中没有对X特征归一化，当学习率较高(>1e-7)时，python数据会爆，再一次说明了特征压缩的重要性

使用scikit-learn实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
x = np.arange(0,19,1)
X_train = x.reshape(-1,1)
y_train = 1+x+x**2

X_norm = scaler.fit_transform(X_train) #特征压缩
print(f"{np.ptp(X_train,axis=0)}") 
print(f"{np.ptp(X_norm,axis=0)}")

sgdr = SGDRegressor(max_iter=1000) #构建线性回归模型
sgdr.fit(X_norm, y_train) #根据所给数据进行训练

b_norm = sgdr.intercept_ #获取训练得到的截断
w_norm = sgdr.coef_ #获取训练得到的系数

y_pred_sgd = sgdr.predict(X_norm)  #得到预测结果

fig,ax=plt.subplots(1,2,figsize=(12,6),sharey=True)
for i in range(len(ax)):
    ax[i].scatter(X_train[:],y_train, label = 'target')
    ax[i].scatter(X_train[:],y_pred_sgd, label = 'predict')
ax[0].set_ylabel("Price"); ax[0].legend()
fig.suptitle("target versus prediction using z-score normalized model")
plt.show()