Machine Learning 4 决策树

决策树

概览

决策树构建过程

• 不断选取一个特征作为判别节点，该特征使得划分后的两个branch的purity最大（即划分得最清晰）

熵

如何衡量一个集合中仅含两类示例的purity呢？这就需要引入熵的概念

熵用于衡量信息的混乱程度：

$H(p) = -plogp \space — \space(1 - p)log(1-p)$

• note:为便于计算，我们定义$'0log0'=0$

扩展到多个类别：

$H(x) = -\sum_{i=1}^{n} p_{i}logp_{i}$

• $P_{1}$:集合中猫占总体的概率

选择特征

如何选取特征呢？

1. 设定问题背景：
   假设数据集 $D$ 中有 $n$ 个样本，样本属于 $k$ 个属性 $\{C_1, C_2, \dots, C_k\}$，每个属性取值个数为${N_{1},N_{2}......N_{k}}$。对于每一个属性 $C_i$，我们希望计算其信息增益 $IG(C_i)$，然后选择信息增益最大的属性作为当前节点的判别类别,其输出类别$Y \in {y_{1}, y_{2}}$

2. 总体信息熵：
   当前节点$father$ 的信息熵 $H(father)$ 为：

   $$H(father) = - \sum_{i=1}^{k} p_i \log p_i$$

   其中，$p_i$ 是类别 $y_i$ 在节点$father$ 中的样本比例。

3. 选取一个类别 $C$：
   每次选取一个属性$C_{i}$ 来计算信息增益。将当前节点 $father$ 按照属于属性 $C_{i}$不同取值 划分为$N_{i}$个子集：

   • $father_j$：样本$C$属性为$n_{j}$ $j\in{1,2...N_{i}}$

   其中，$|father_j|$ 是 $C$的属性值为$n_{j}$样本数

4. 条件熵计算：
   根据类别 $C_{i}$ 的划分计算条件熵 $H(father| C_{i})$，即按属性 $C_i$ 划分后的加权熵：

   $$H(father | C_{i}) = \sum_{j=1}^{N_{i}}\frac{|father_j|}{|father|} H(father_{j})$$

5. 信息增益：
   类别 $C_i$ 的信息增益 $IG(C_i)$ 计算为：

   $$IG(C_i) = H(father) - H(father | C_i)$$

6. 选取信息增益最大的类别：
   计算所有类别 $C_1, C_2, \dots, C_k$ 的信息增益，选择信息增益最大的类别 $C_{\text{best}}$ 作为当前节点的判别类别：

   $$C_{\text{best}} = \arg\max_{i} IG(C_i)$$

7. 继续递归：
   根据选中的判别类别 $C_{\text{best}}$ 将数据集划分为子集，并递归执行以上步骤，直到满足终止条件。

信息增益(information gain)：

$g(D,A) = H(D) - H(D|A)$

• 已知随机变量A的值的前提下，随机变量D信息熵的减少量
• $H(D|A) = \sum_{i=1}^{n} P(a_{i})H(D|A=a_{i})$ 也被称为条件熵

在该实例中即为$H(p_{root}) - w_{left}H(p_{left}) -w_{right}H(p_{right})$

• 当一个离散属性有k种取值
  • 方式一：建立k个分支
  • 方式二：one-hot编码，转变为k个属性，每个属性取值0或1

处理连续变量

上述特征都是针对于属性是离散的，例如动物要么有卷毛，要么没卷毛。但如果是连续的属性比如动物的体重呢？

假设$X$是连续的变量，则可以考虑以$X <= k$作为判别节点的特征

• 选择不同的阈值$k$计算信息增益，选取其中k使得信息增益最大的作为结果

构建树

参数调整以防过拟合

• 树的高度（不希望太高）

• 节点内信息熵值若低于某个阈值则停止递归

• 节点内的data数量（若已经很少，则没必要继续往下细分）

回归树

即预测输出cat or not cat，而是具体的一个数值

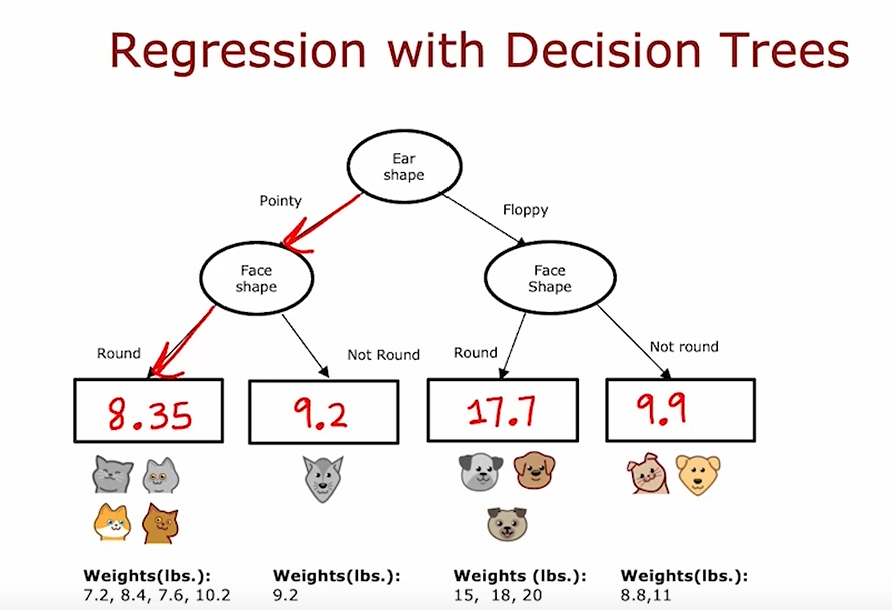
则输出即是叶节点中所有$X$ 对应 $y$ 的平均值

• 选取特征的依据，从节点的信息熵改为方差