核心思想
已知输入数据X X X { x 1 , x 2 , . . . . . . x n } \{x_1, x_2, ......x_n\} { x 1 , x 2 , ...... x n }
假设一个隐式变量z z z
希望训练一个生成器X ^ = g ( z ) \hat X = g(z) X ^ = g ( z ) X ^ \hat X X ^
从Auto Encoder到Variational Auto-Encoder
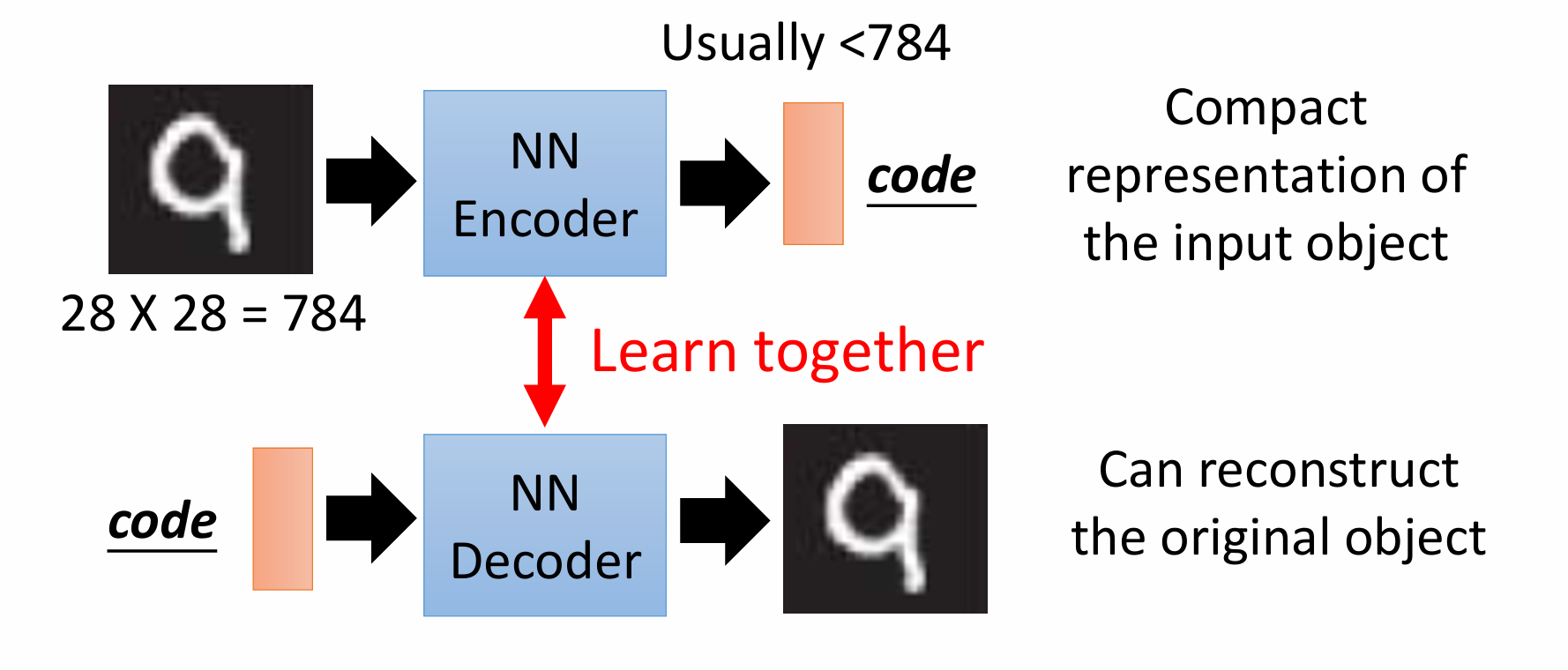
原始的AE思想很简单
用encoder原数据压缩,压缩后的特征可视作隐式变量z,之后再用decoder还原
AE的缺点:
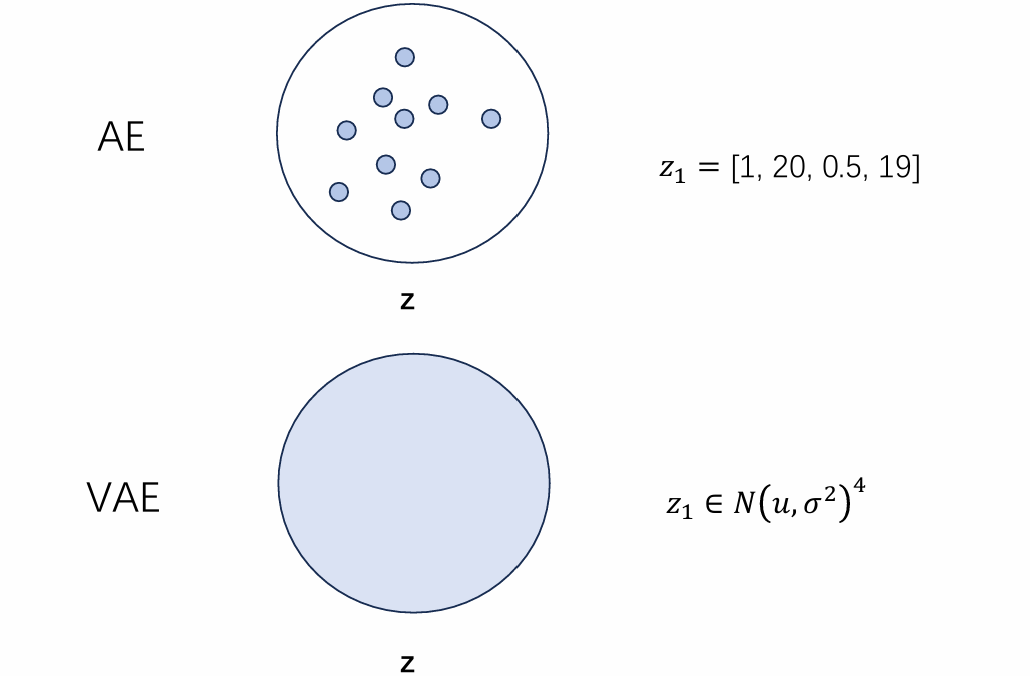
AE压缩后的特征z是离散的(可以视作{ z 1 , z 2 , . . . z n } \{z_1, z_2, ...z_n\} { z 1 , z 2 , ... z n } z 1 = [ 1 , 20 , 0.5 , 19 ] z_1 = [1,20,0.5,19] z 1 = [ 1 , 20 , 0.5 , 19 ]
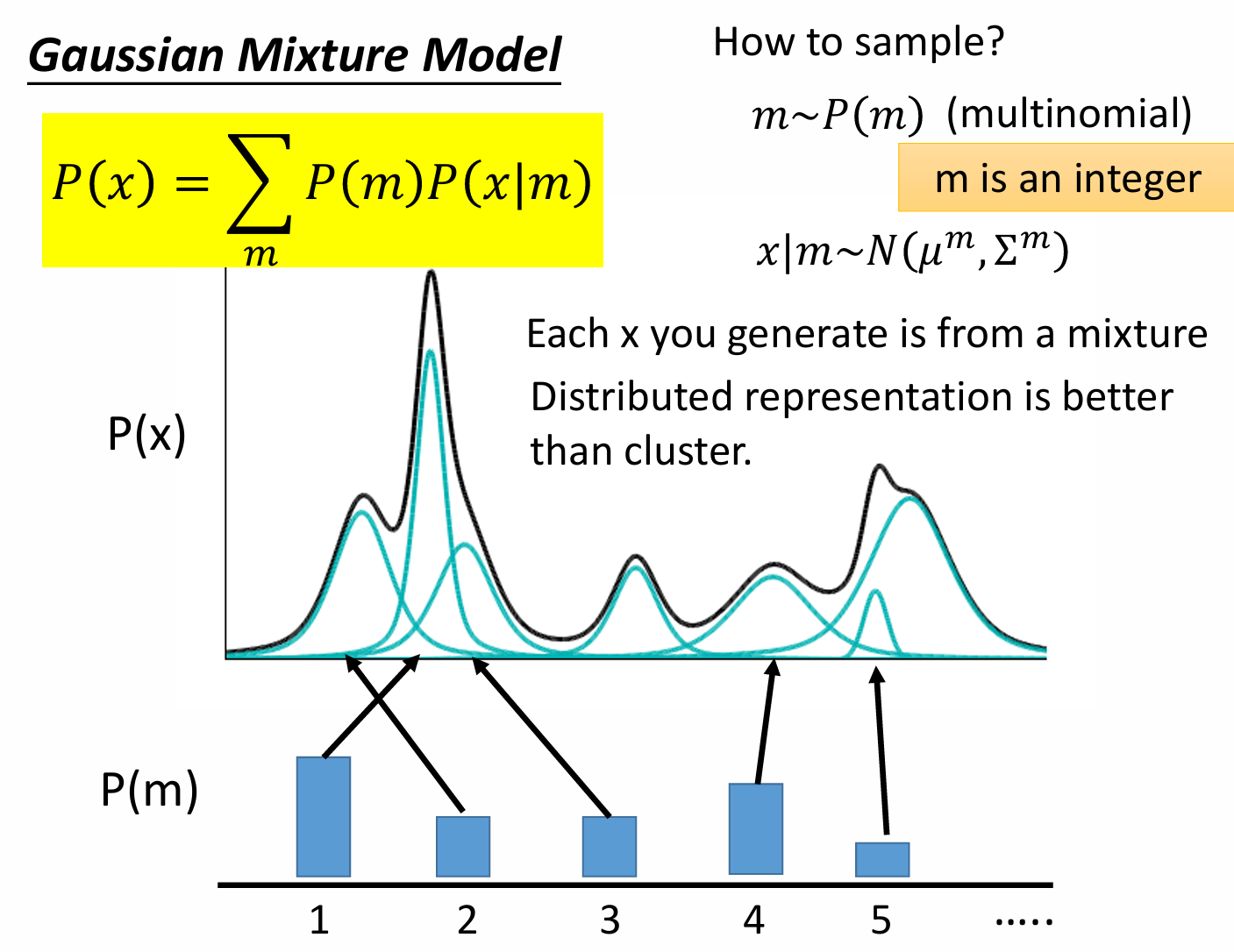
解释说明: P ( X ) = ∑ z P ( X ∣ z ) P ( z ) P(X) = \sum_z P(X|z)P(z) P ( X ) = ∑ z P ( X ∣ z ) P ( z )
基于该离散 的方式所能生成的P ( X ) P(X) P ( X )
ok,想到这里,要想获得好的生成 , 我们想尽可能地扩大隐式变量z的空间,怎么做呢?
VAE:
与其让神经网络生成基于样本x对应的特征z(一个向量),我们不如让神经网络学习基于样本x的隐式z的分布 (一个分布)不就好了嘛
接下来就是我们的VAE之旅
VAE实现
回顾目标,学习P ( X ) P(X) P ( X )
VAE提出先验知识:假设隐式变量z ∼ N ( 0 , I ) z \sim N (0,I) z ∼ N ( 0 , I ) x ∣ z ∼ N ( u ( z ) , σ ( z ) ) x|z \sim N(u(z), \sigma (z)) x ∣ z ∼ N ( u ( z ) , σ ( z ))
根据全概率公式转化为
P ( X ) = ∫ z P ( X ∣ z ) P ( z ) d z P(X) = \int_z P(X|z)P(z)dz P ( X ) = ∫ z P ( X ∣ z ) P ( z ) d z
我们采用对数最大似然估计的方式,求解生成器g g g θ \theta θ
L ( θ ) = ∑ x l o g p θ ( x ) = ∑ x l o g ∫ z p θ ( x ∣ z ) p ( z ) d z L(\theta) = \sum _x logp_{\theta}(x) =\sum_x log\int_z p_{\theta}(x|z)p(z)dz
L ( θ ) = x ∑ l o g p θ ( x ) = x ∑ l o g ∫ z p θ ( x ∣ z ) p ( z ) d z
其中 p ( z ) p(z) p ( z ) x x x z z z x x x
但由于我们不知道p ( z ) p(z) p ( z ) 引入一个可控简单的分布 q ( z ) q(z) q ( z ) q ( z ) q(z) q ( z ) x x x
改写为:
log p θ ( x ) = ∫ z q ( z ) log p θ ( x ) d z \begin{align*}
\log p_{\theta}(x) = \int_z q(z) \log p_{\theta}(x) \, dz
\end{align*}
log p θ ( x ) = ∫ z q ( z ) log p θ ( x ) d z
注意:上式对任何分布q ( z ) q(z) q ( z ) q ( z ) q(z) q ( z )
log p θ ( x ) = ∫ z q ( z ) log p θ ( x ) d z = ∫ z q ( z ) ⋅ log [ p θ ( x ∣ z ) p θ ( z ) p θ ( z ∣ x ) ⋅ q ( z ) q ( z ) ] d z = ∫ z q ( z ) [ log p θ ( x ∣ z ) + log p θ ( z ) q ( z ) + log q ( z ) p θ ( z ∣ x ) ] d z = E z ∼ q ( z ) log p θ ( x ∣ z ) − D KL ( q ( z ) ∥ p θ ( z ) ) ⏟ ELBO + D KL ( q ( z ) ∥ p θ ( z ∣ x ) ) ⏟ KL ≥ [ E z ∼ q ( z ) log p θ ( x ∣ z ) − D KL ( q ( z ) ∥ p θ ( z ) ) ] (ELBO) \begin{align*}
\log p_{\theta}(x)
&= \int_z q(z) \log p_{\theta}(x) \, dz \\
&= \int_z q(z) \cdot \log \left[ \frac{p_{\theta}(x|z) p_{\theta}(z)}{p_{\theta}(z|x)} \cdot \frac{q(z)}{q(z)} \right] dz \\
&= \int_z q(z) \big[ \log p_{\theta}(x|z) + \log \frac{p_{\theta
}(z)}{q(z)} + \log \frac{q(z)}{p_{\theta}(z|x)} \big] dz \\
&= \underbrace{\mathbb{E}_{z \sim q(z)} \log p_{\theta}(x|z)
- D_{\text{KL}}(q(z) \| p_{\theta}(z))}_{\text{ELBO}}
+ \underbrace{D_{\text{KL}}(q(z) \| p_{\theta}(z|x))}_{\text{KL}} \\
&\geq \big[ \mathbb{E}_{z \sim q(z)} \log p_{\theta}(x|z) - D_{\text{KL}}(q(z) \| p_{\theta}(z)) \big] \quad \text{(ELBO)}
\end{align*}
log p θ ( x ) = ∫ z q ( z ) log p θ ( x ) d z = ∫ z q ( z ) ⋅ log [ p θ ( z ∣ x ) p θ ( x ∣ z ) p θ ( z ) ⋅ q ( z ) q ( z ) ] d z = ∫ z q ( z ) [ log p θ ( x ∣ z ) + log q ( z ) p θ ( z ) + log p θ ( z ∣ x ) q ( z ) ] d z = ELBO E z ∼ q ( z ) log p θ ( x ∣ z ) − D KL ( q ( z ) ∥ p θ ( z )) + KL D KL ( q ( z ) ∥ p θ ( z ∣ x )) ≥ [ E z ∼ q ( z ) log p θ ( x ∣ z ) − D KL ( q ( z ) ∥ p θ ( z )) ] (ELBO)
KL散度用于衡量一个分布p p p q q q
D K L ( p ∣ ∣ q ) = E p ( x ) l o g [ p ( x ) q ( x ) ] D_{KL}(p||q) = \mathbb E_{p(x) }log[\frac{p(x)}{q(x)}] D K L ( p ∣∣ q ) = E p ( x ) l o g [ q ( x ) p ( x ) ]
EM算法
学长已经说的很好了
EM Algorithm - xyfJASON
总结EM
E-step:取q ( z ) = p θ ( z ∣ x ) q(z) = p_\theta(z|x) q ( z ) = p θ ( z ∣ x )
M-step: 固定q(z),优化θ \theta θ
从EM到VAE
但在VAE中,取q ( z ) = p θ ( z ∣ x ) q(z) = p_\theta(z|x) q ( z ) = p θ ( z ∣ x ) p θ ( z ∣ x ) p_\theta(z|x) p θ ( z ∣ x )
但E-step很巧妙在于,当我们固定θ \theta θ ,l o g p θ ( x ) logp_{\theta }(x) l o g p θ ( x ) 是固定的 ,即 E L B O + K L ELBO + KL E L BO + K L
虽然我们无法直接求出令KL = 0的p θ ( z ∣ x ) p_\theta(z|x) p θ ( z ∣ x ) 通过最大化ELBO来隐式地最小化KL ,从而使得我们的q(z)逼近p θ ( z ∣ x ) p_\theta(z|x) p θ ( z ∣ x )
最终的损失函数
故VAE中采取的做法是将原始的EM转化为
E-step:固定θ \theta θ q ( z ) q(z) q ( z )
M-step:固定q ( z ) q(z) q ( z ) θ \theta θ
又因为最开始的推导与q ( z ) q(z) q ( z ) q ( z ) q(z) q ( z ) ϕ \phi ϕ q ϕ ( z ∣ x ) q_{\phi} (z|x) q ϕ ( z ∣ x )
同时假设x x x p ( z ) p(z) p ( z ) N ( 0 , I ) N(0,I) N ( 0 , I )
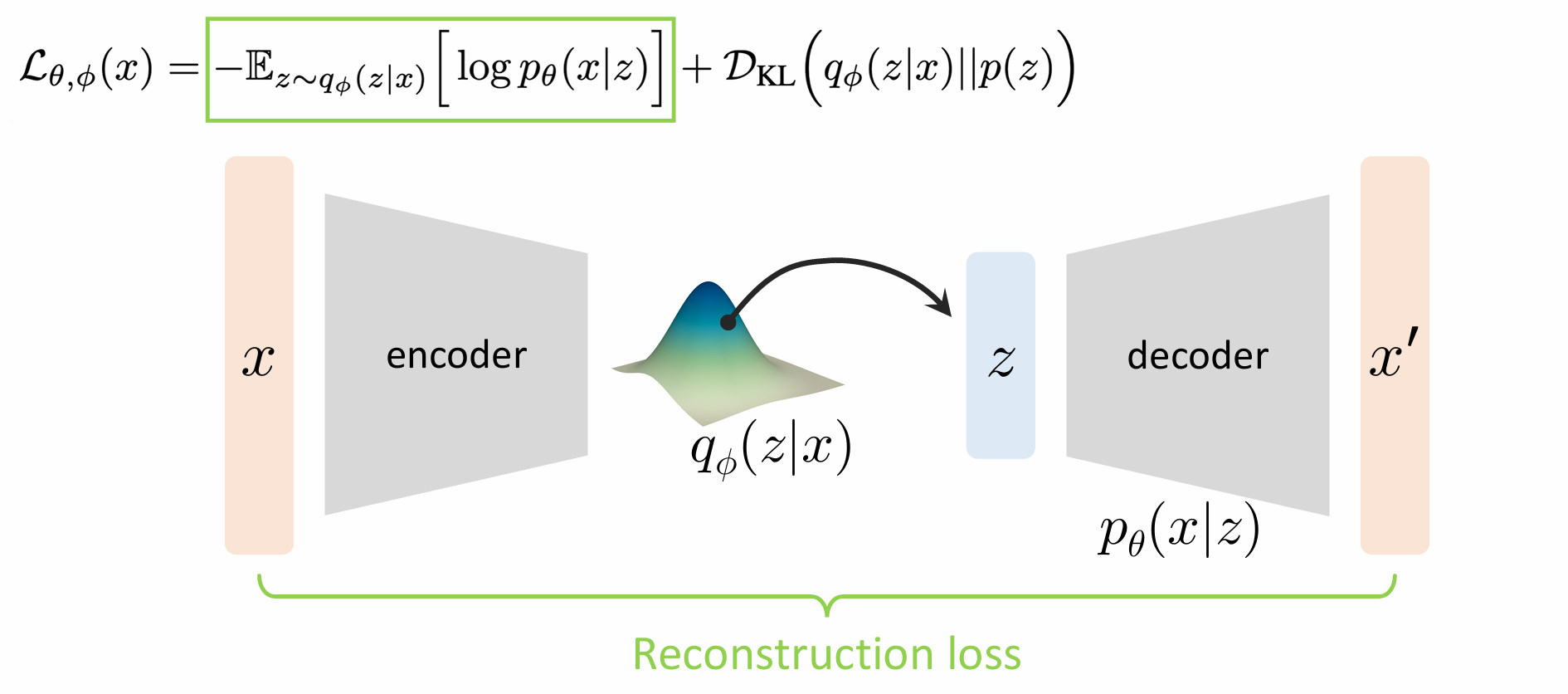
由于两个都是最大化ELBO,且在使用梯度下降法时每次更新都是基于上一次的参数做调整,与这里的固定异曲同工。故VAE的Loss函数可以写为-ELBO
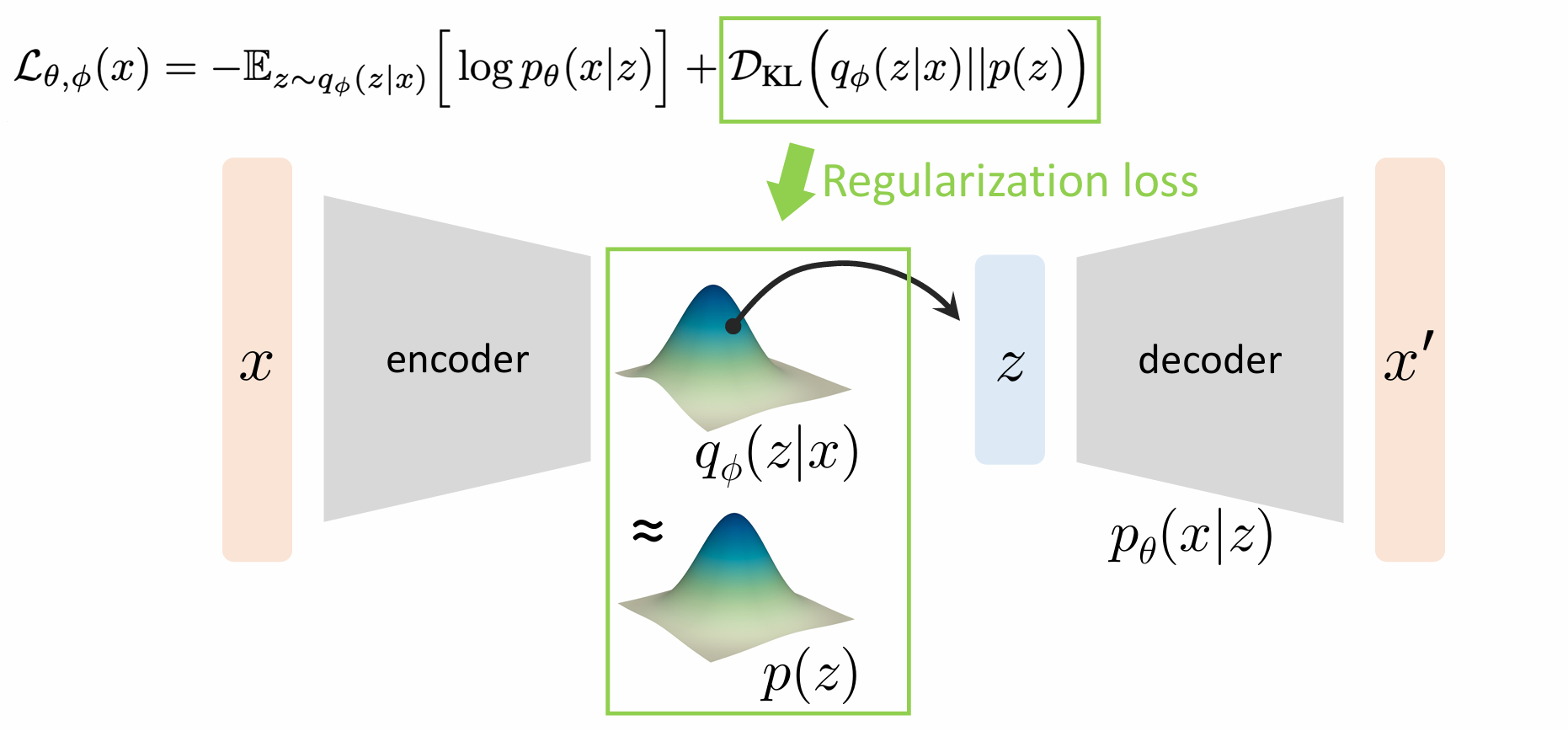
L θ , ϕ ( x ) = − E L B O = − E z ∼ q ϕ ( z ∣ x ) l o g p θ ( x ∣ z ) + D K L ( q ϕ ( z ∣ x ) ∣ ∣ p ( z ) ) \mathcal{L}_{\theta, \phi}(x)= -ELBO = -E_{z\sim q_{\phi}(z|x)} logp_{\theta}(x|z) + D_{KL}(q_{\phi}(z|x)||p(z)) L θ , ϕ ( x ) = − E L BO = − E z ∼ q ϕ ( z ∣ x ) l o g p θ ( x ∣ z ) + D K L ( q ϕ ( z ∣ x ) ∣∣ p ( z ))
将高斯分布带入化简可得MSE:
M S E ( x , u θ ( z ) ) MSE(x, u_{\theta}(z))
MSE ( x , u θ ( z ))
两个高斯分布的KL散度公式推导:
注意:对于连续变量的最大似然估计时,我们采用的是概率密度而不是概率
假设P ∼ N ( u p , σ p ) , Q ∼ N ( u q , σ q ) P \sim N(u_p, \sigma_p), Q\sim N(u_q, \sigma_q) P ∼ N ( u p , σ p ) , Q ∼ N ( u q , σ q )
D K L ( P ∣ ∣ Q ) = ∫ z p ( z ) log 1 2 π σ p 2 e − ( z − μ p ) 2 2 σ p 2 1 2 π σ q 2 e − ( z − μ q ) 2 2 σ q 2 d z = ∫ z p ( z ) [ 1 2 log ( σ q 2 σ p 2 ) − ( z − μ p ) 2 2 σ p 2 + ( z − μ q ) 2 2 σ q 2 ] d z . \begin{align*}D_{KL}(P || Q) &= \int_z p(z) \log \frac{\frac{1}{\sqrt{2\pi \sigma_p^2}} e^{-\frac{(z-\mu_p)^2}{2\sigma_p^2}}}{\frac{1}{\sqrt{2\pi \sigma_q^2}} e^{-\frac{(z-\mu_q)^2}{2\sigma_q^2}}} dz \\&= \int_z p(z) \left[ \frac{1}{2} \log\left(\frac{\sigma_q^2}{\sigma_p^2}\right) - \frac{(z-\mu_p)^2}{2\sigma_p^2} + \frac{(z-\mu_q)^2}{2\sigma_q^2} \right] dz.\end{align*} D K L ( P ∣∣ Q ) = ∫ z p ( z ) log 2 π σ q 2 1 e − 2 σ q 2 ( z − μ q ) 2 2 π σ p 2 1 e − 2 σ p 2 ( z − μ p ) 2 d z = ∫ z p ( z ) [ 2 1 log ( σ p 2 σ q 2 ) − 2 σ p 2 ( z − μ p ) 2 + 2 σ q 2 ( z − μ q ) 2 ] d z .
逐项计算:
第一项:
∫ z p ( z ) 1 2 log ( σ q 2 σ p 2 ) d z = 1 2 log ( σ q 2 σ p 2 ) \int_z p(z) \frac{1}{2} \log\left(\frac{\sigma_q^2}{\sigma_p^2}\right) dz = \frac{1}{2} \log\left(\frac{\sigma_q^2}{\sigma_p^2}\right) ∫ z p ( z ) 2 1 log ( σ p 2 σ q 2 ) d z = 2 1 log ( σ p 2 σ q 2 )
第二项:
∫ z p ( z ) ( z − μ p ) 2 2 σ p 2 d z = 1 2 σ p 2 ∫ z p ( z ) ( z − μ p ) 2 d z = 1 2 σ p 2 Var ( P ) = 1 2 . \begin{align*}\int_z p(z) \frac{(z-\mu_p)^2}{2\sigma_p^2} dz &= \frac{1}{2\sigma_p^2} \int_z p(z) (z-\mu_p)^2 dz \\&= \frac{1}{2\sigma_p^2} \operatorname{Var}(P) = \frac{1}{2}.\end{align*} ∫ z p ( z ) 2 σ p 2 ( z − μ p ) 2 d z = 2 σ p 2 1 ∫ z p ( z ) ( z − μ p ) 2 d z = 2 σ p 2 1 Var ( P ) = 2 1 .
第三项:
∫ z p ( z ) ( z − μ q ) 2 2 σ q 2 d z = 1 2 σ q 2 ∫ z p ( z ) [ z 2 − 2 μ q z + μ q 2 ] d z = 1 2 σ q 2 [ σ p 2 + μ p 2 − 2 μ q μ p + μ q 2 ] . \begin{align*}\int_z p(z) \frac{(z-\mu_q)^2}{2\sigma_q^2} dz &= \frac{1}{2\sigma_q^2} \int_z p(z) \left[z^2 - 2\mu_q z + \mu_q^2 \right] dz \\&= \frac{1}{2\sigma_q^2} \left[\sigma_p^2 + \mu_p^2 - 2\mu_q \mu_p + \mu_q^2 \right].\end{align*} ∫ z p ( z ) 2 σ q 2 ( z − μ q ) 2 d z = 2 σ q 2 1 ∫ z p ( z ) [ z 2 − 2 μ q z + μ q 2 ] d z = 2 σ q 2 1 [ σ p 2 + μ p 2 − 2 μ q μ p + μ q 2 ] .
综上:
D K L ( P ∣ ∣ Q ) = 1 2 [ log ( σ q 2 σ p 2 ) + σ p 2 σ q 2 + ( μ p − μ q ) 2 σ q 2 − 1 ] D_{KL}(P || Q) = \frac{1}{2} \left[ \log\left(\frac{\sigma_q^2}{\sigma_p^2}\right) + \frac{\sigma_p^2}{\sigma_q^2} + \frac{(\mu_p - \mu_q)^2}{\sigma_q^2} - 1 \right] D K L ( P ∣∣ Q ) = 2 1 [ log ( σ p 2 σ q 2 ) + σ q 2 σ p 2 + σ q 2 ( μ p − μ q ) 2 − 1 ]
如果P,Q服从多维高斯分布
D KL ( P ∥ Q ) = 1 2 [ log det Σ p det Σ q + tr ( Σ q − 1 Σ p ) + ( μ p − μ q ) ⊤ Σ q − 1 ( μ p − μ q ) − d ] \begin{align*}D_{\text{KL}}(P \| Q) = \frac{1}{2} \Big[ \log \frac{\det \Sigma_p}{\det \Sigma_q} + \operatorname{tr}(\Sigma_q^{-1} \Sigma_p) + (\mu_p - \mu_q)^\top \Sigma_q^{-1} (\mu_p - \mu_q)- d\Big]\end{align*} D KL ( P ∥ Q ) = 2 1 [ log det Σ q det Σ p + tr ( Σ q − 1 Σ p ) + ( μ p − μ q ) ⊤ Σ q − 1 ( μ p − μ q ) − d ]
将P ∼ N ( u ϕ , σ ϕ ) P \sim N(u_{\phi}, \sigma_{\phi}) P ∼ N ( u ϕ , σ ϕ ) Q ∼ N ( 0 , I ) Q \sim N(0,I) Q ∼ N ( 0 , I )
在实际VAE实现中简化为不同维度是独立的,故协方差矩阵只有对角线上存在值。公式简化为d个一维高斯分布的散度之和
D K L ( q ϕ ( z ∣ x ) ∣ ∣ N ( 0 , I ) ) = ∑ i = 1 d 1 2 [ l o g ( σ ϕ i ) 2 + σ ϕ i 2 + u ϕ i 2 − 1 ] D_{KL}(q_{\phi}(z|x)|| N(0,I)) = \sum^d_{i=1} \frac{1}{2}[log(\sigma_{\phi_i})^2 + \sigma_{\phi_i}^2 + u_{\phi_i}^2 -1]
D K L ( q ϕ ( z ∣ x ) ∣∣ N ( 0 , I )) = i = 1 ∑ d 2 1 [ l o g ( σ ϕ i ) 2 + σ ϕ i 2 + u ϕ i 2 − 1 ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 class VAE (torch.nn.Module):def __init__ (self, input_dim, hidden_dims, decode_dim=-1 , use_sigmoid=True ):''' input_dim: The dimensionality of the input data. hidden_dims: A list of hidden dimensions for the layers of the encoder and decoder. decode_dim: (Optional) Specifies the dimensions to decode, if different from input_dim. ''' super ().__init__()1 ] // 2 int )def add_encoder_layer (name: str , layer: torch.nn.Module ) -> None :f"{name} {counts[name]} " , layer))1 def add_decoder_layer (name: str , layer: torch.nn.Module ) -> None :f"{name} {counts[name]} " , layer))1 for x in hidden_dims:"mlp" , torch.nn.Linear(input_channel, x))"relu" , torch.nn.LeakyReLU())1 ]for x in decoder_dims:"mlp" , torch.nn.Linear(input_channel, x))"relu" , torch.nn.LeakyReLU())1 ], self.z_size),1 ], self.z_size),1 ], input_dim),def encode (self, x ):return mean, logvardef reparameterize (self, mean, logvar, n_samples_per_z=1 ):0.5 * logvar).to(device) return zdef decode (self, z ):return outdef forward (self, x, n_samples_per_z=1 ):if n_samples_per_z > 1 :1 ).expand(batch_size, n_samples_per_z, latent_dim)1 ).expand(batch_size, n_samples_per_z, latent_dim)1 )1 ])return {"imgs" : x_probs,"z" : z,"mean" : mean,"logvar" : logvar128 , 64 , 36 , 18 , 18 ]256 1 , input_dim]).to(device)with torch.no_grad():print (test_out)
重构损失就是MSE在此略,正则损失则为:
1 2 3 4 5 6 7 8 9 10 def loss_KL_wo_E (output ):'logvar' ])'logvar' ]'mean' ]return -0.5 * torch.sum (torch.pow (mean, 2 )1.0 - logvar,1 ])
思考
l o s s loss l oss 重构损失 和先验约束
重构损失 保证不同x x x p θ ( z ∣ x ) p_{\theta}(z|x) p θ ( z ∣ x ) N ( 0 , I ) N(0,I) N ( 0 , I ) 先验约束 保证学习到的p θ ( z ∣ x ) p_{\theta}(z|x) p θ ( z ∣ x )
问题:
当真实的p θ ( z ∣ x ) p_{\theta}(z|x) p θ ( z ∣ x )
重构损失使得模型输出倾向于输出平均,限制了模型对复杂数据分布,造成图像模糊