从DDPM到DDIM

回顾DDPM

DDPM前提假设：

• 遵循马可夫链

  前向固定:

  $$q(x_{0:T}) = q(x_0)\prod_{t=T}^{1} q(x_t|x_{t-1})$$

  后向:

  $$p_{\theta}(x_{0:T}) = p_{\theta}(x_T)\prod_{t=T}^{1} p_{\theta}(x_{t-1}|x_t)$$

• 定义加噪过程 ： $q(x_t|x_{t-1}) = \mathcal N(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_t I)$

• 损失函数:

$$\begin{aligned} \mathcal{L}(\theta) &= -\mathbb{E}_{z \sim q(x_{1:T} | x_0)} \log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T} | x_0)} \\ &= -\mathbb{E}_{z \sim q(x_{1:T} | x_0)} \log \frac{p_{\theta}(x_T) \cdot p_{\theta}(x_0 | x_1) \prod_{t=2}^{T} p_{\theta}(x_{t-1} | x_t)}{q(x_T | x_0) \prod_{t=2}^{T} q(x_{t-1} | x_t, x_0)} \end{aligned}$$

• 分母写成$q(x_{T}|x_0)$ 和$q(x_{t-1}|x_t, x_0)$,为什么写成这种形式?
• 我们想反向的时候预测前向传播的噪声，但前向传播的噪声是$q(x_{t}|x_{t-1})$,是后面依赖前面的形式，但反向时候是依赖反过来的，不能直接将$q(x_{t}|x_{t-1})$作为预测目标。所以我们要求出 $q(x_{t-1}|x_t, x_0)$关于噪声的表达式，然后让反向的时候预测。
• $q(x_{T}|x_0)$ 是前向传播已知， $q(x_{t-1}|x_t, x_0)$是我们想求出来的表达式，是反向的时候预测的目标

DDPM的具体推导详见xyfson学长的blog:DDPM，本文只是简要介绍背景和motivation

Motivation

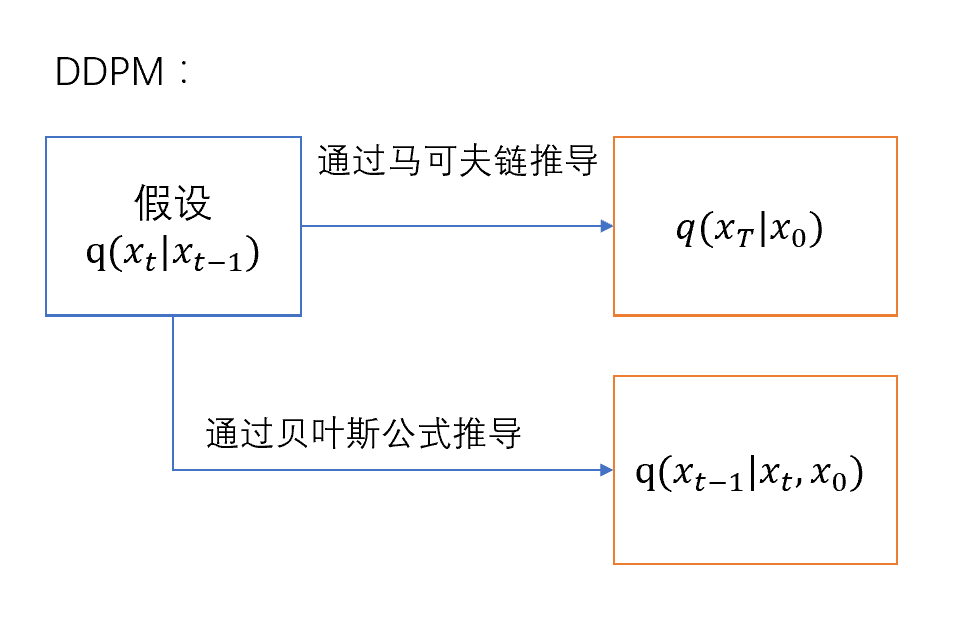
• 注意到DDPM由于马可夫链假设的限制，反向传播时不得不一步步预测，导致反向预测的时间步往往很长，速度很慢
• DDPM中的损失函数中并没有直接出现我们的假设$q(x_t|x_{t-1})$

大胆的想法：

能否绕过$q(x_t|x_{t-1})$和马可夫链，没必要一步步预测，直接定义$q(x_{t-1}|x_t, x_0)$ 和$q(x_{T}|x_0)$ ？

DDIM

DDIM为了与DDPM对齐，定义:

$$q(x_T|x_0) = \mathcal N (x_t; \sqrt{\bar\alpha}x_0, (1 - \bar \alpha)I )$$

通过约束$q(x_t-1|x0) = \int q(x_{t-1}|x_t, x_0) q(x_t|x_0)dx$ 求得$q(x_{t-1}|x_t, x_0)$的解，之后就和DDPM一样了。由于没有马可夫链的限制，反向可以只选择原DDPM时间步的一个子集进行训练和预测，大大提高速度。

具体推导见详见xyfson学长的blog：DDIM与加速采样