Diffusion models

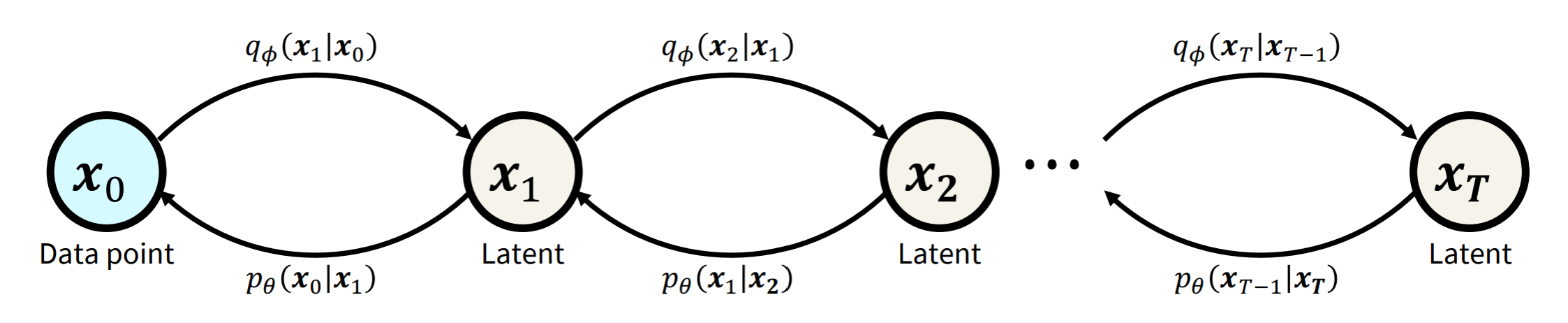
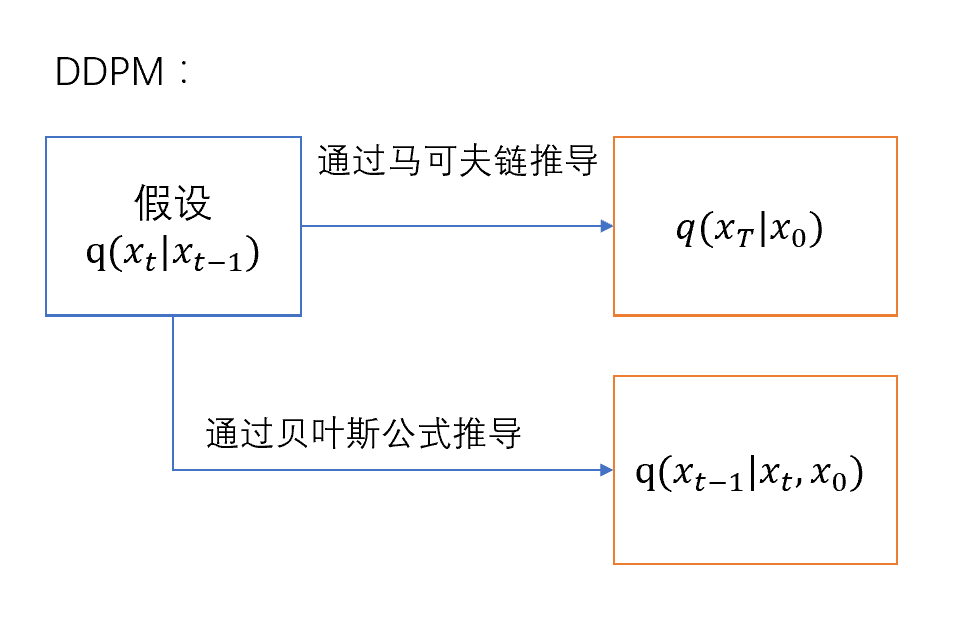
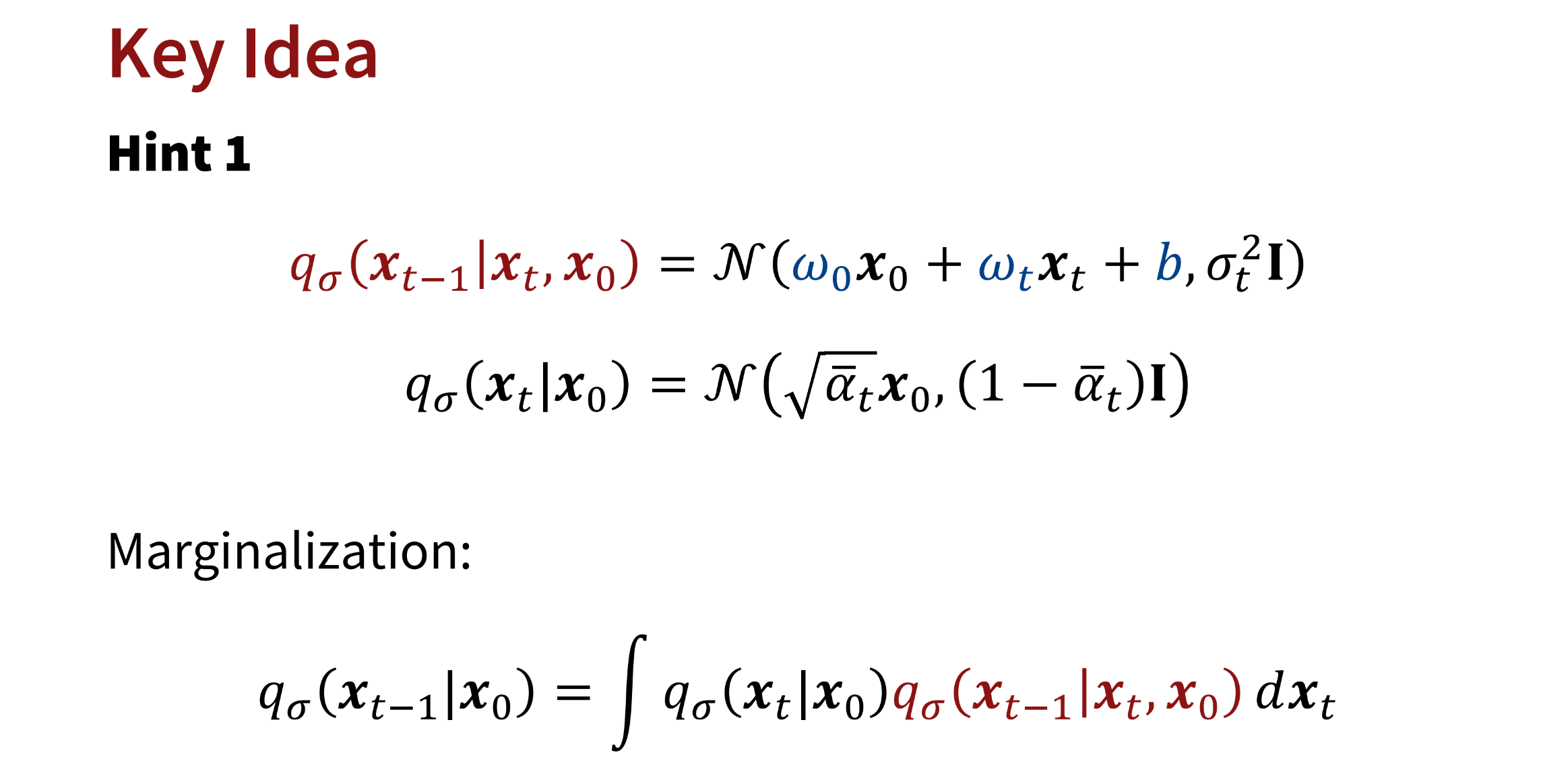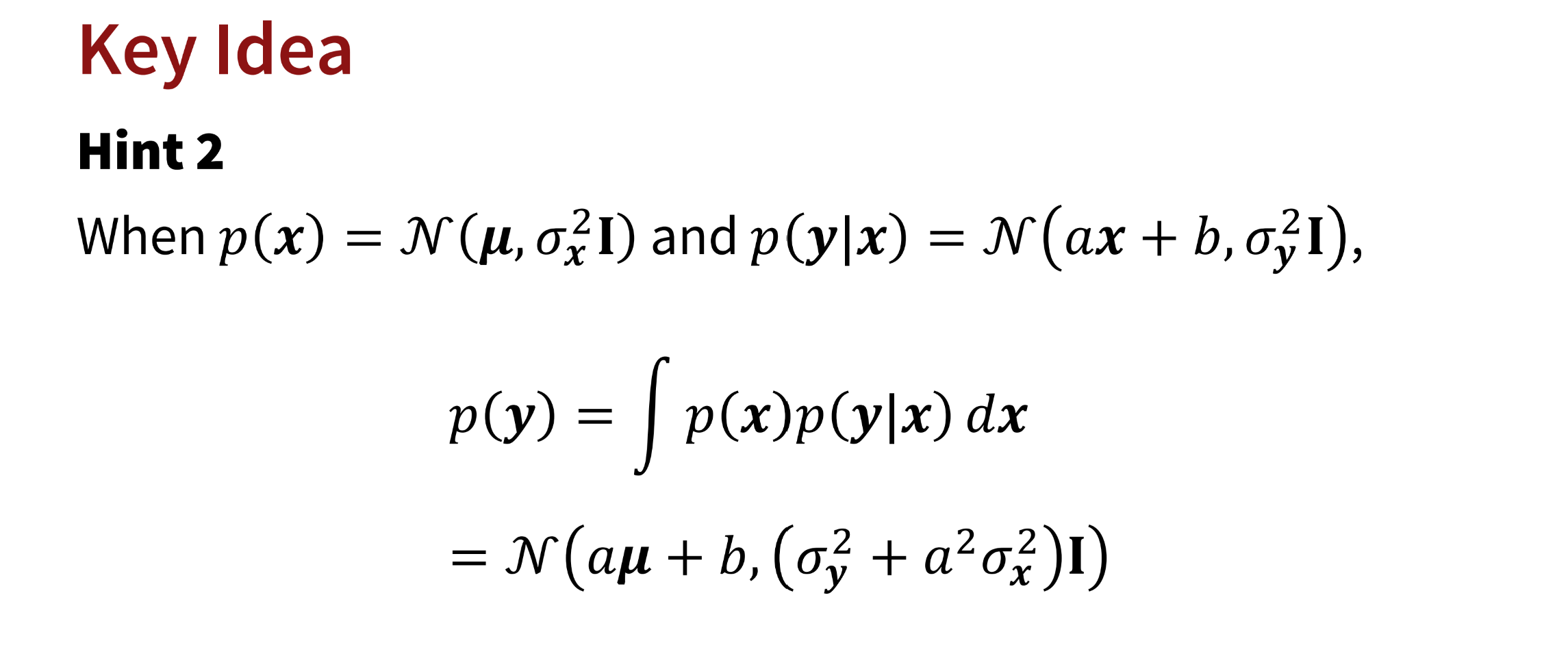DDPM

Brief Intro

从VAE的角度来看，VAE中只有一层隐变量，而DDPM将$x_0$视为data point， 而$x_{1:T}$整体作为隐变量，是一种Hierarchical VAEs

Assumptions

• 遵循马可夫链

  前向predefined:

  $$q(x_{0:T}) = q(x_0)\prod_{t=T}^{1} q(x_t|x_{t-1})$$

  • predefined 加噪过程 ： $q(x_t|x_{t-1}) = \mathcal N(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_t I)$

  后向learn:

  $$p_{\theta}(x_{0:T}) = p_{\theta}(x_T)\prod_{t=T}^{1} p_{\theta}(x_{t-1}|x_t)$$

DDPM定义前向传播 $q(x_t|x_{t-1}) = \mathcal N(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_t I)$(读者看到这里不免有一个疑问，为什么要定义为这种形式？之后会介绍以Score Matching角度和SDE角度来理解)

故$x_t = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon$

令$\alpha_t = 1 - \beta_t$

则$x_t = \sqrt{\alpha_t}x_{t-1} + \sqrt{(1-\alpha_t)}\epsilon$

$x_{t-1} = \sqrt{\alpha_{t-2}}x_{t-2} + \sqrt{1-\alpha_{t-1}}\epsilon$

由于正态分布性质不难推出$x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$

$q(x_t|x_0) = \mathcal N(x_0, \sqrt{\bar{\alpha}_t}x_0, {1-\bar\alpha_{t}}I)$

Loss Function

其ELBO推导：

$$\begin{align*} \log p({x}_0) &= \log \int p_\theta({x}_{0:T}) d{x}_{1:T} \\ &= log \int p_\theta({x}_{0:T}) \frac{q_{\phi}(\mathbf{x}_{1:T}|x_0)}{q_{\phi}(\mathbf{x}_{1:T}|x_0)}dx_{1:T} \\ &= log\mathbb E_{q_{\phi}(x_{1:T}|x_0)}[ \frac{p_\theta({x}_{0:T})}{q_{\phi}(\mathbf{x}_{1:T}|x_0)}]\\ & \ge \mathbb E_{q_{\phi}(x_{1:T}|x_0)}log[ \frac{p_\theta({x}_{0:T})}{q_{\phi}(\mathbf{x}_{1:T}|x_0)}] \end{align*}$$

最后一步的推导来自于Jensen 不等式

对于一个凹函数 $f(x)$，Jensen 不等式可以表述为：

$$f\left( \mathbb{E}[X] \right) \geq \mathbb{E}\left[ f(X) \right]$$

其中：

• $f(x)$是凹函数。
• $x$是随机变量。

这次推导与上篇VAE形式略有不同，但本质相同，最后一步差的就是$D_{KL}(q_{\phi}(x_{1:T}|x_0)||p(x_{1:T}|x_0))$

不妨换一种方式，以$\color{red}{D_{KL}(q_{\phi}(x_{1:T}|x_0)||p(x_{1:T}|x_0))}$ 开始推导

$$\begin{aligned}{D_{KL}(q_{\phi}(x_{1:T}|x_0)||p(x_{1:T}|x_0))}&= \mathbb E_{q_{\phi}(x_{1:T}|x_0)}[log\frac{q_{\phi}(x_{1:T}|x_0)}{p(x_{1:T}|x_0)}] \\&= \mathbb E_{q_{\phi}(x_{1:T}|x_0)}[log\frac{q_{\phi}(x_{1:T}|x_0)}{\frac{p(x_{0:T})}{p(x_0)}}]\\&= \mathbb E_{q_{\phi}(x_{1:T}|x_0)}[log\frac{q_{\phi}(x_{1:T}|x_0)p(x_0)}{p(x_{0:T})}]\\&= E_{q_{\phi}(x_{1:T}|x_0)}[logp(x_0)] + E_{q_{\phi}(x_{1:T}|x_0)}[logq_{\phi}(x_{1:T}|x_0)] - E_{q_{\phi}(x_{1:T}|x_0)}[logp(x_{0:T})]\\&= logp(x_0) + E_{q_{\phi}(x_{1:T}|x_0)}[logq_{\phi}(x_{1:T}|x_0)] - E_{q_{\phi}(x_{1:T}|x_0)}[logp(x_{0:T})]\\&= logp(x_0) + E_{q_{\phi}(x_{1:T}|x_0)}[log\frac{q_{\phi}(x_{1:T}|x_0)}{p(x_{0:T})}] \end{aligned}$$

损失函数:

$$\begin{aligned} \mathcal{L}(\theta) &= -\mathbb{E}_{z \sim q(x_{1:T} | x_0)} \log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T} | x_0)} \\ &= -\mathbb{E}_{z \sim q(x_{1:T} | x_0)} \log \frac{p_{\theta}(x_T) \cdot p_{\theta}(x_0 | x_1) \prod_{t=2}^{T} p_{\theta}(x_{t-1} | x_t)}{q(x_T | x_0) \prod_{t=2}^{T} q(x_{t-1} | x_t, x_0)} \\ &= -\underbrace{\mathbb{E}_{x_1 \sim q(x_1|x_0)} \left[\log p_{\theta}(x_0 | x_1) \right]}_{\text{reconstruction}} + \underbrace{\sum_{t=2}^{T} \mathbb{E}_{x_t \sim q(x_t|x_{t-1}, x_0)} \left[ D_{\text{KL}}(q(x_{t-1} | x_t, x_0) \Vert p_{\theta}(x_{t-1} | x_t)) \right]}_{\text{matching}} + \underbrace{D_{\text{KL}}(q(x_T | x_0) \Vert p_{\theta}(x_T))}_{\text{regularization}} \end{aligned}$$

为什么在损失函数中将前向过程$q$改写成$q(x_{T}|x_0)$ 和$q(x_{t-1}|x_t, x_0)$的形式？

因为损失函数作用是反向传播阶段，前向传播是$q(x_{t}|x_{t-1})$,是时间序列由小到大的形式，而反向时候是时间序列由大到小，不能直接将$q(x_{t}|x_{t-1})$作为预测目标。

因此我们要求出改写前向传播为时间序列由大到小的形式，这里最终推导出来是 $q(x_{t-1}|x_t, x_0)$

具体推导：

DDPM假设遵循马尔科夫链，因此$q(x_t|x_{t-1}) = q(x_t|x_{t-1},x_0)$

又因为$q({x}_{t}, {x}_{t-1} | {x}_0) = q({x}_{t} | {x}_{t-1}, {x}_0) \cdot q({x}_{t-1} | {x}_0).$

$$\begin{aligned}q(x_{1:T} | x_0) &= q(x_1|x_0)\prod_{t=2}^{T}q(x_t|x_{t-1}) \\&= q(x_1|x_0)\prod_{t=2}^{T}q(x_t|x_{t-1},x_0)\\&= q(x_1|x_0)\prod_{t=2}^{T}\frac{q({x}_{t}, {x}_{t-1} | {x}_0)}{q({x}_{t-1} | {x}_0)} \\&= q(x_1|x_0)\prod_{t=2}^{T}\frac{q({x}_{t}|x_0)q({x}_{t-1} |x_t, {x}_0)}{q({x}_{t-1} | {x}_0)} \\&= q(x_T|x_0)\prod_{t=2}^{T}q(x_{t-1}|x_t, x_0)\end{aligned}$$

总结： $q(x_{T}|x_0)$ 是前向传播已知， $q(x_{t-1}|x_t, x_0)$是推导出来的时间序列由大到小的表达式，是反向的时候预测的目标

首先查看损失函数第三项prior loss

作者希望$T-> \infty$, $q(x_T|x_0)= \mathcal N(x_0; \sqrt{\bar{\alpha_T}}x_0, {1-\alpha_{T}}I)$ 收敛到$N(x_0;0,I)$

因此要求$\alpha_t$ 递减，使得$\lim_{t \to \infty} \bar{\alpha_t} = 0$, 这也说明了为什么$\beta_t$要递增

由于$q(x_T|x_0)$= $p_{\theta}(x_T)$是predefined, 因此第三项=0

再看第二项matching loss

$$D_{\text{KL}}(q(x_{t-1} | x_t, x_0) \Vert p_{\theta}(x_{t-1} | x_t))$$

$q(x_t|x_{t-1}) = \mathcal N(x_t;\sqrt{\alpha_t}x_{t-1}, 1-\alpha_t I)$

$q(x_t|x_0) = \mathcal N(x_0, \sqrt{\bar{\alpha}_t}x_0, {1-\bar\alpha_{t}}I)$

$q(x_{t-1}|x_0) = \mathcal N(x_0, \sqrt{\bar{\alpha}_{t-1}}x_0, {1-\bar\alpha_{t-1}}I)$

$$\begin{align*} q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) &= q(\boldsymbol{x}_t|\boldsymbol{x}_{t-1}) \frac{q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_0)}{q(\boldsymbol{x}_t|\boldsymbol{x}_0)} \\ &\propto \exp\Biggl( -\frac{1}{2} \biggl( \frac{(\boldsymbol{x}_t - \sqrt{\alpha_t}\boldsymbol{x}_{t-1})^2}{1 - \alpha_t} + \frac{(\boldsymbol{x}_t - \sqrt{\overline{\alpha}_{t-1}}\boldsymbol{x}_0)^2}{1 - \overline{\alpha}_{t-1}} - \frac{(\boldsymbol{x}_t - \sqrt{\overline{\alpha}_t}\boldsymbol{x}_0)^2}{1 - \overline{\alpha}_t} \biggr) \Biggr) \\ &= \ \cdots \\ &= \mathcal{N}\left( \widetilde{\mu}(\boldsymbol{x}_t, \boldsymbol{x}_0),\ \widetilde{\sigma}_t^2\mathbf{I} \right) \quad \text{\color{blue}Another normal distribution!} \end{align*}$$

• 通过将上式展开，求解一元二次方程的根，我们得到$u(x_t,x_0)$， 将二次项的系数求倒数，便得到方差$\tilde \sigma_t$
• where $\tilde{\mu}(x_t, x_0) = \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t + \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0$ and $\tilde{\sigma}_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t$.
• 将$x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$带入
• $\tilde u(x_t, x_0) = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \frac{1- \alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon)$

由于前向传播$q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{x}_0) = \mathcal{N}\left( \widetilde{\mu}(\boldsymbol{x}_t, \boldsymbol{x}_0),\ \widetilde{\sigma}_t^2\mathbf{I} \right)$

因此DDPM中在后向传播作者定义相同的形式$p_{\theta}(x_{t-1} | x_t) = \mathcal{N}\left( {\mu_{\theta}}(\boldsymbol{x}_t, \boldsymbol{t}),\ {\sigma}_t^2\mathbf{I} \right)$

特别地，这里${\sigma}_t$作者取和前向传播相同，即$\sigma_t^2 = \tilde{\sigma}_t^2 = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t$

mean-predictor

两个方差相同的正态分布做KL散度，根据公式则为

$$D_{\text{KL}}(q(x_{t-1} | x_t, x_0) \Vert p_{\theta}(x_{t-1} | x_t)) = \frac{1}{2\sigma_t^2}||\tilde{\mu}(x_t, x_0) - {\mu_{\theta}}(x_t, t) ||_2^2$$

$x_0$-predictor

$\tilde{\mu}(x_t, x_0) = \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t + \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} x_0$, 第一项对于前向和后向传播均相同，故我们可以将上式改写为

$$D_{\text{KL}}(q(x_{t-1} | x_t, x_0) \Vert p_{\theta}(x_{t-1} | x_t)) = \frac{\bar{\alpha}_t\beta_t^2}{2\sigma_t^2(1 - \bar{\alpha}_t)^2}||x_0- x_{\theta}(x_t, t) ||_2^2$$

$\epsilon$-predictor

$\tilde u(x_t, x_0) = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \frac{1- \alpha_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon)$

$$D_{\text{KL}}(q(x_{t-1} | x_t, x_0) \Vert p_{\theta}(x_{t-1} | x_t)) = \frac{(1-\alpha_t)^2}{2\sigma_t^2{\bar{\alpha}}_t(1-\bar{\alpha}_t)}||\epsilon_t- \epsilon_{\theta}(x_t, t) ||_2^2$$

• 通常在实际训练中，前面的系数可以忽略变为1

最后第一项reconstruction loss

即重构损失，本质上和第二项损失相同，可以合并

最终的损失函数

$$\mathbb{E}_{x_0\sim q(x_0) ,t>1, q(x_t|x_0)}[||\epsilon_t - \epsilon_{\theta}(x_t,t)||_2^2]$$

• 而当t=1时，通常不固定，部分方法采取直接预测$x_0$。

Traning

Generation

• 采样方法实际上为Langevin Dynamics Sampling， 还额外增加一个随机力$z$

Experiment Result

在AFHQ数据集的cat类别 32x32图像分辨率下，训练150,000个steps后，采样2k张图片FID约为45左右

采样结果如下：

DDIM

Motivation

• 注意到DDPM由于马可夫链假设的限制，反向传播时不得不一步步预测，导致反向预测的时间步往往很长，速度很慢
• DDPM中的损失函数中并没有直接出现我们的假设$q(x_t|x_{t-1})$, 而只用到了$q({x}_{t}, {x}_{t-1} | {x}_0)$

大胆的想法：

能否绕过$q(x_t|x_{t-1})$和马可夫链，没必要一步步预测，直接定义$q(x_{t-1}|x_t, x_0)$ ？

有读者可能会问，DDPM的损失函数不是用到了马尔科夫链的性质吗，事实上DDIM并不是直接拿DDPM的损失公式来用，而是假设

$$q_\sigma(x_{1:T} | x_0) = q_\sigma(x_T | x_0) \prod_{t=2}^T q_\sigma(x_{t-1} | x_t, x_0)$$

进一步证明了DDIM和DDPM损失函数之差是一个常数

Method

DDIM中作者定义

$q_{\sigma}(x_t|x_{t-1},x_0) = \mathcal N(w_0 x_0 + w_tx_t + b, \sigma_t^2I)$

如何确定系数$w_0$, $w_t$, $b$ ?

作者希望从 $q_{\sigma}(x_t|x_{t-1},x_0)$ 推导得出的$q_{\sigma}(x_t|x_0)$ 仍然和DDPM中的形式一样，即$q(x_t|x_0) = \mathcal N(x_0, \sqrt{\bar{\alpha}_t}x_0, {1-\bar\alpha_{t}}I)$

考虑更简单的情形，已知

• $q_{\sigma}(x_t|x_{t-1},x_0) = \mathcal N(w_0 x_0 + w_tx_t + b, \sigma_t^2I)$
• $q(x_t|x_0) = \mathcal N(x_0, \sqrt{\bar{\alpha}_t}x_0, {1-\bar\alpha_{t}}I)$

如何保证$q(x_{t-1}|x_0) = \mathcal N(x_0, \sqrt{\bar{\alpha}_{t-1}}x_0, {1-\bar\alpha_{t-1}}I)$ ？

由此推导得到

$$\begin{align*} q(x_{t-1}|x_0) &= \mathcal N(x_0, \sqrt{\bar{\alpha}_{t-1}}x_0, {1-\bar\alpha_{t-1}}I)\\ &= \mathcal N(x_0, w_0x_0 + w_t\sqrt{\bar{\alpha}_t}x_0 + b, (\sigma_t^2+w_{t}^2({1-\bar\alpha_{t}}))I) \end{align*}$$

不妨令 $b$ = 0

$w_t = \sqrt{\frac{1- \bar{\alpha}_{t-1} - \sigma_t^2}{(1-\bar{\alpha}_t)}}$

$w_0 = \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\bar{\alpha}_{t}}\sqrt{\frac{1- \bar{\alpha}_{t-1} - \sigma_t^2}{(1-\bar{\alpha}_t)}}$

带入$q_{\sigma}(x_t|x_{t-1},x_0) = \mathcal N(w_0 x_0 + w_tx_t + b, \sigma_t^2I)$

最终得到

令$\sigma_t = \eta \tilde{\sigma}_t = \eta \sqrt{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t}$

• $\eta$ = 1, DDIM退化为DDPM，是一个马尔可夫链过程
• $\eta$ = 0, DDIM的反向扩散都变为确定性过程

注意，从始至终本文DDIM中并没有讨论前向传播的过程，因为理论上DDIM是作为在采样时的一种策略，通常仍然使用DDPM训练。

事实上，当方差为0时，其对应的隐式前向传播不再是随机采样，而是通过反向过程的逆运算计算得到，涉及到ODE， 具体可见DDIM Inversion

其反向扩散过程的确定性是指，一旦给出采样出$x_T$， 那其generate出的$x_0$一定相同，因为我们没有随机力$z$

Faster Sampling

相较于训练时采取的总时间步$T$，DDIM使得采样生成时可以选择一个$T$的子序列$[t_{s1}, t_{s2} ...t_{sk}]$ ，进行上方的反向扩散即可

DDIM Inversion

当标准差为0时

$$x_{0|t} = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t - \sqrt{1 - \bar{\alpha}_t}\epsilon_{\theta}(x_t,t))$$

$$\begin{align} x_{t-1} &= \sqrt{\bar{\alpha}_{t-1}}x_{0|t} + \sqrt{1 - \bar{\alpha}_{t-1}}\epsilon_{\theta}(x_t,t)) \\ &=\sqrt{\bar{\alpha}_{t-1}}[\frac{1}{\sqrt{\bar{\alpha}_{t}}}x_t + (\sqrt{\frac{1}{\bar{\alpha}_{t-1}}-1} - \sqrt{\frac{1}{\bar{\alpha}_{t}}-1}) \epsilon_{\theta}(x_t,t)] \end{align}$$

则

$$\begin{align} x_{t-1} - x_t &= \sqrt{\bar{\alpha}_{t-1}}x_{0|t} + \sqrt{1 - \bar{\alpha}_{t-1}}\epsilon_{\theta}(x_t,t)) \\ &=\sqrt{\bar{\alpha}_{t-1}}[(\frac{1}{\sqrt{\bar{\alpha}_{t}}} - \frac{1}{\sqrt{\bar{\alpha}_{t-1}}})x_t + (\sqrt{\frac{1}{\bar{\alpha}_{t-1}}-1} - \sqrt{\frac{1}{\bar{\alpha}_{t}}-1}) \epsilon_{\theta}(x_t,t)] \end{align}$$

我们已经得到$x_{t_1} - x_{t2}$的通用表达式后，基于$\Delta t$很小的假设，我们可以将$x_{t+1} - x_t$直接带入得到

$$\begin{align} x_{t+1} - x_t &= \sqrt{\bar{\alpha}_{t+1}}x_{0|t} + \sqrt{1 - \bar{\alpha}_{t+1}}\epsilon_{\theta}(x_t,t)) \\ &=\sqrt{\bar{\alpha}_{t+1}}[(\frac{1}{\sqrt{\bar{\alpha}_{t}}} - \frac{1}{\sqrt{\bar{\alpha}_{t+1}}})x_t + (\sqrt{\frac{1}{\bar{\alpha}_{t+1}}-1} - \sqrt{\frac{1}{\bar{\alpha}_{t}}-1}) \epsilon_{\theta}(x_t,t)] \end{align}$$

应用：

图像编辑：

• CFG扩散模型对图像做DDIM inversion后得到z， 利用z经过新的文本，使用CFG扩散模型得到编辑后的图像。但当CFG使用的w过大时，存在失真现象，原因就在于权重w会导致错误累积。
• Null-text: 先使用CFG w=1扩散模型对图像DDIM inversion后得到$z$， 再使用w=7.5的CFG文本扩散模型DDIM inversion后得到$z^{*}$, 然后设置只有空文本Null对应的token可被优化，最小化$z$和$z^{*}$ 之间的距离，保证w很大时的隐空间也可以被良好的重建

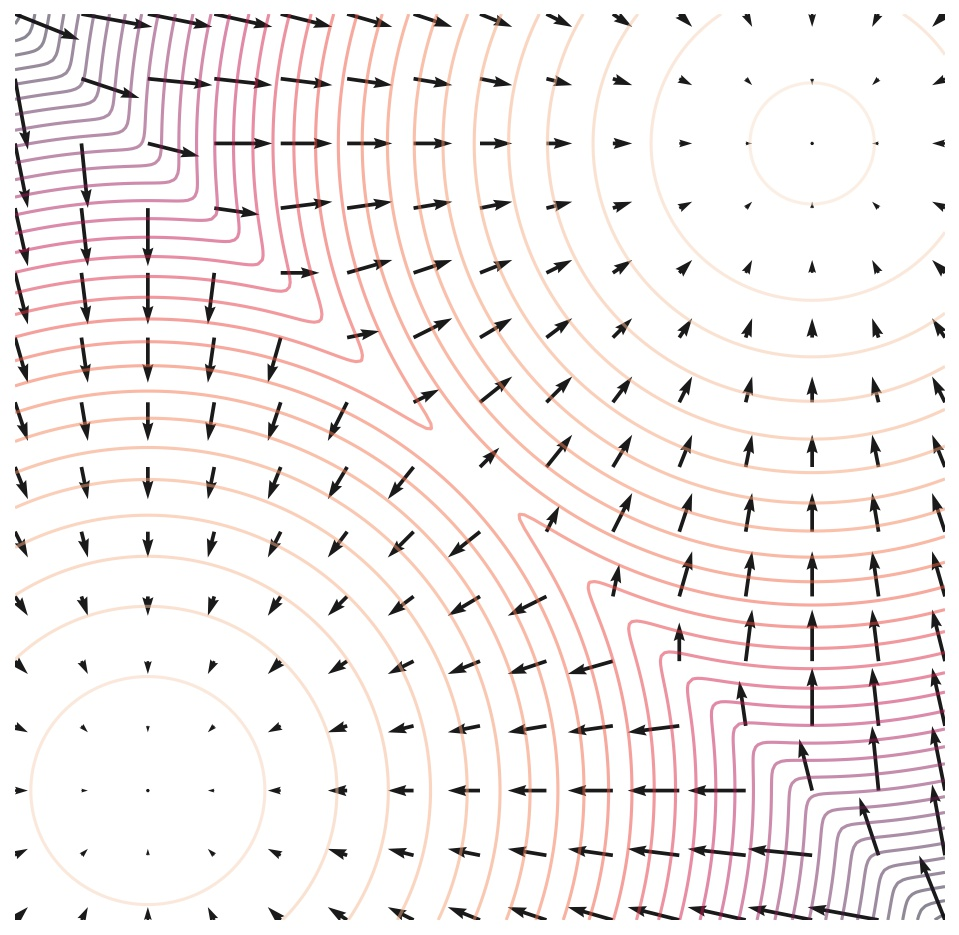
Score Matching

Score function

Energy-based model 定义了使用函数模拟概率密度函数PDF的基本形式

$$p(x) = \frac{e^{-f_{\theta}(x)}}{Z_{\theta}}$$

PDF中的两个约束

• 在$x$的每个data point上函数值非负
• 在$x$空间积分等于1

$Z_{\theta}$起的就是归一化的作用

然而实际情况由于$x$分布的复杂性，归一化因子$Z_{\theta}$很难学，因此引出Score model

Score-based model

$$s_{\theta}(x)=\nabla_{x}logp_{\theta}(x) = \nabla_{x}log\frac{e^{-f(x)}}{Z_{\theta}} = -\nabla_{x}f_{\theta}(x)$$

很高兴地，令人讨厌的$Z_{\theta}$消失了

由此，Score Matching是通过匹配原始PDF导数和模型学出来$s_{\theta}(x)$来对原始PDF建模

$$\mathcal{L}(\theta) = \frac{1}{2}E_{x\sim p(x)}||\nabla_{x}logp(x) - s_{\theta}(x)||_2^2$$

只要模型能够很好地拟合出函数的导数，那对这个导数求积分就是我们想得到的PDF

• 具体地，在空间中任意采样一点$x_0$, $s_{\theta}(x)$就表示当前$x_{0}$朝目标数据分布$x_{data}$所需要移动的向量步

然而，由于我们不知道真实的$p(x)$，自然$\nabla_{x}logp(x)$也无从得知。

接下来需要利用数学上的一些tricks来简化：

start:

$$\mathcal{L}(\theta) = \frac{1}{2}E_{x\sim p(x)}||\nabla_{x}logp(x) - s_{\theta}(x)||_2^2$$

goal:

$$\begin{align*} \mathcal{L}(\theta) &= \frac{1}{2}\mathbb{E}_{p(x)}[s_{\theta}(x)^2] + \mathbb{E}_{p(x)}[\nabla_{x}s_{\theta}(x)] \end{align*}$$

完整推导过程：

首先平方和展开为三项

$$\begin{align*}\mathcal{L}(\theta) &= \frac{1}{2}E_{x\sim p(x)}||\nabla_{x}logp(x) - s_{\theta}(x)|_2^2| \\&= \frac{1}{2} \int p(x)[(\nabla_{x}logp(x))^2 + s_{\theta}(x)^2 - 2\nabla_{x}logp(x)s_{\theta}(x)]dx \\&= \frac{1}{2} \int p(x)(\nabla_{x}logp(x))^2dx + \frac{1}{2} \int p(x)s_{\theta}(x)^2 dx -\int p(x)\nabla_{x}logp(x)s_{\theta}(x)dx \\\end{align*}$$

第一项由于和$s_{\theta}(x)$无关，训练时可以忽略

对于最后一项

$$\begin{align}\int p(x)\nabla_{x}logp(x)s_{\theta}(x)dx &= \int\nabla_{x}p(x)s_{\theta}(x)dx \\&= p(x)s_{\theta}(x)|_{-inf}^{inf} - \int p(x)\nabla_{x}s_{\theta}(x)dx \\&= 0 - \int p(x)\nabla_{x}s_{\theta}(x)dx \quad \\\end{align}$$

• (1):$\nabla_{x}logp(x)$ 改写为 $\frac{\nabla_x p(x)}{p(x)}$
• (2): 分部积分
• (3):$p(x)$在x无穷大时趋近于0

带入损失函数最终得到

$$\begin{align*}\mathcal{L}(\theta) &= \frac{1}{2} \int p(x)s_{\theta}(x)^2 dx + \int p(x)\nabla_{x}s_{\theta}(x)dx \\&= \frac{1}{2}\mathbb{E}_{p(x)}[s_{\theta}(x)^2] + \mathbb{E}_{p(x)}[\nabla_{x}s_{\theta}(x)]\end{align*}$$

Problems

• Expensive Traning：注意损失函数第二项实际上为雅可比矩阵，计算量极大
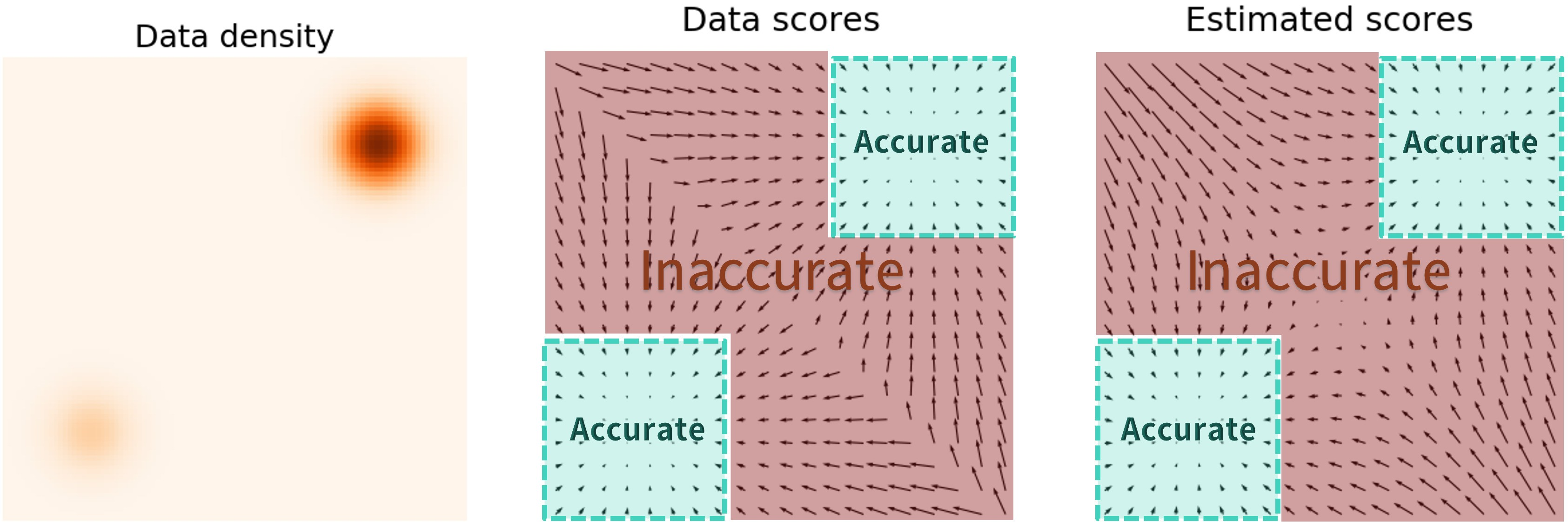
• Low Converage of Data Space

Noise

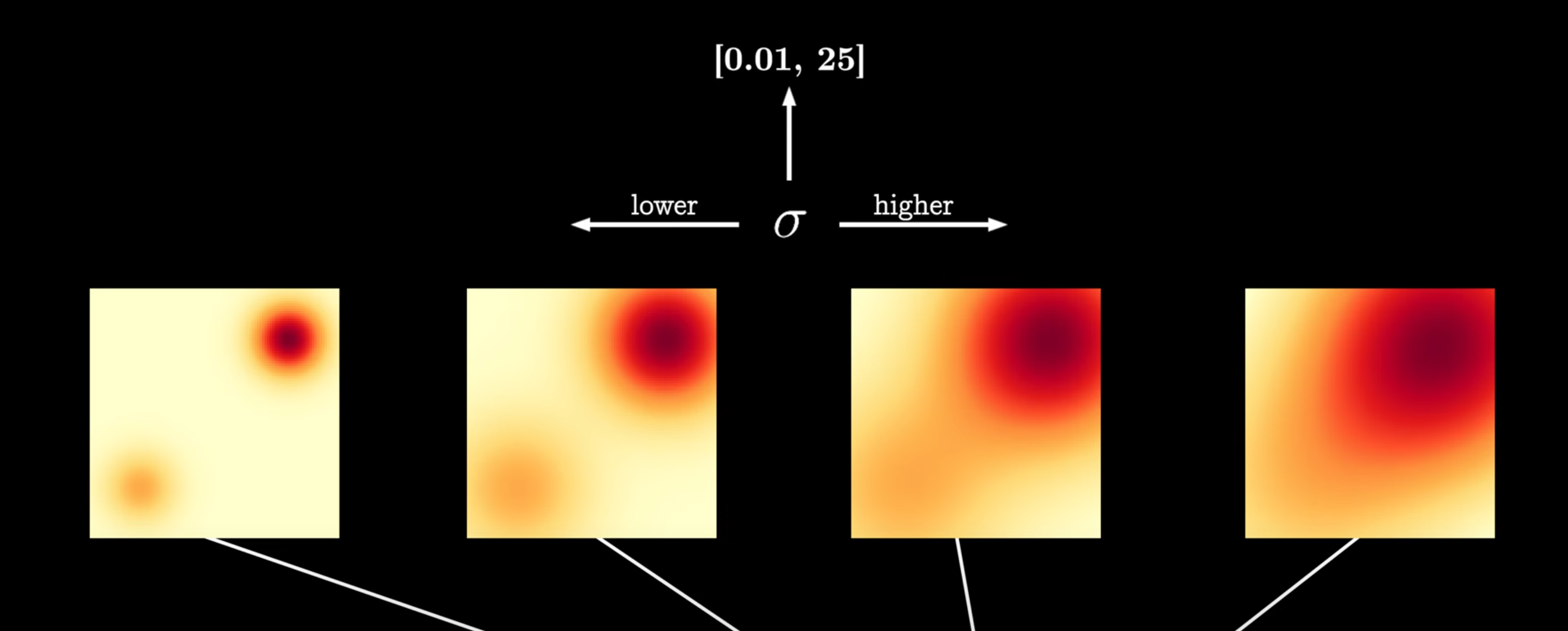
数据空间覆盖得少，怎么办？先对数据加Noise！

$\tilde x = x + \epsilon$ , $\epsilon \sim N(0, \sigma^2 I)$

添加的扰动对应方差大训练见到的数据空间就多，方差小见到的数据就少

$p(x) \to p_{\sigma}(x)$

这便得到了 Noise Conditional Score-based Model

但这只解决了Low Converage of Data Space的问题, 那Expensive Traning呢？

Denoising Score Matching

start:

$$\mathcal{L}(\theta) = \frac{1}{2}E_{\tilde x\sim p_{\sigma}(\tilde x)}||\nabla_{\tilde x}logp_{\sigma}(\tilde x) - s_{\theta}(\tilde x)||_2^2$$

goal:

$$\mathcal{L}(\theta) = \frac{1}{2}\mathbb{E}_{x\sim p(x), \tilde x \sim p_{\sigma}(\tilde x)}||\nabla_{\tilde x}logp_{\sigma}(\tilde x|x) - s_{\theta}(\tilde x)||_2^2$$

完整推导过程

平方项展开与之前相同

第三项化简：

$$\begin{align}\int p_{\sigma}(\tilde x)\nabla_{\tilde x}logp(\tilde x)s_{\theta}(\tilde x)dx &= \int\nabla_{\tilde x}p_{\sigma}(\tilde x)s_{\theta}(\tilde x)d\tilde x \\&= \int\nabla_{\tilde x}\textcolor{red}{(\int p(x)p_{\sigma}(\tilde x|x)dx)}s_{\theta}(\tilde x)d\tilde x \\&= \int\textcolor{red}{(\int p(x)\nabla_{\tilde x}p_{\sigma}(\tilde x|x)dx)}s_{\theta}(\tilde x)d\tilde x \\&= \int\int p(x)\textcolor{red}{p_{\sigma}(\tilde x|x)\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)}\textcolor{blue}{s_{\theta}(\tilde x)}dxd\tilde x \\\end{align}$$

• (5): 利用边缘概率分布的定义
• (6): 莱布尼兹积分规则
• (7): $\nabla_x p(x)$改写为$p(x)\nabla_{x}logp(x)$ , 积分顺序变换

带入损失函数变为

$$\begin{align}\mathcal{L}(\theta)&= \frac{1}{2} \mathbb{E}_{\tilde x\sim p_{\sigma}(\tilde x)}||\nabla_{\tilde x}logp_{\sigma}(\tilde x)||_2^2 + \frac{1}{2} \mathbb{E}_{\tilde x\sim p_{\sigma}(\tilde x)}||s_{\theta}(\tilde x)||_2^2 - \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}||\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)s_{\theta}(\tilde x)||\\\end{align}$$

让我们关注后面两项

$$\begin{align*}&\frac{1}{2} \mathbb{E}_{\tilde x\sim p_{\sigma}(\tilde x)}||s_{\theta}(\tilde x)||_2^2 - \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}||\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)s_{\theta}(\tilde x)||_2^2 \\&= \frac{1}{2} \mathbb{E}_{\textcolor{red}{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}}||s_{\theta}(\tilde x)||_2^2 - \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}||\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)s_{\theta}(\tilde x)||_2^2 \\&= \frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}[||s_{\theta}(\tilde x)^2 - 2\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)s_{\theta}(\tilde x)||] \\&= \frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}[||s_{\theta}(\tilde x)^2 - 2\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)s_{\theta}(\tilde x) + \textcolor{red}{\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)^2 - \nabla_{\tilde x}logp_{\sigma}(\tilde x|x)^2}||] \\&= \frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}||\textcolor{red}{s_{\theta}(\tilde x) -\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)}||_2^2 - \frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}[\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)^2]\end{align*}$$

再次带入损失函数

$$\begin{align*}\mathcal{L}(\theta)&= \frac{1}{2} \mathbb{E}_{\tilde x\sim p_{\sigma}(\tilde x)}||\nabla_{\tilde x}logp_{\sigma}(\tilde x)||_2^2 +\frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}||{s_{\theta}(\tilde x) -\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)}||_2^2 - \frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}[\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)^2] \\\end{align*}$$

省略与score model无关的首尾两项：

$$\begin{align*}\mathcal{L}(\theta)&= \frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}||{s_{\theta}(\tilde x) -\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)}||_2^2 \\\end{align*}$$

你可能会疑惑，那这样$\nabla_{\tilde x}logp_{\sigma}(\tilde x|x)$ ，不还是需要计算梯度？那计算量怎么会减少？

但我们实际思考，$\tilde x = x + \epsilon$, 故$p_{\sigma}(\tilde x|x) = \frac{1}{(2\pi)^{d/2}\sigma^2} e^{-1/2\sigma^2|\tilde x - x|^2}$

$\nabla_{\tilde x}logp_{\sigma}(\tilde x|x) = \frac{1}{\sigma^2}(x-\tilde x) = -\frac{1}{\sigma^2}\epsilon$ ,梯度仅仅是两个向量的差！运算量大大减少

$$\begin{align*} \mathcal{L}(\theta) &= \frac{1}{2} \mathbb{E}_{x \sim p(x), \tilde x \sim p_{\sigma}(\tilde x|x)}||{s_{\theta}(\tilde x) + \frac{1}{2} \epsilon}||_2^2 \\ \end{align*}$$

Sampling

ok,训练过程已经介绍完了。我们在inference时如何生成图像呢，答案就是采样。

随机在空间选取一data point， 使用score model预测方向，移动一小步，如此往复

Simple Sample:

$$\tilde x_{t+1} = \tilde x_{t} + \alpha s_{\theta}(\tilde x_t)$$

• 缺点:最终所有的data point都很可能收敛到数据平均值，而不是数据分布的真实样本

Langevin Dynamics Sampling

引入随机力，这种扰动有助于采样器探索目标分布的其他模态，而不仅仅是集中在数据均值上

$${\tilde x}_{t+1} = \tilde x_t + \alpha s_{\theta}(\tilde x_t)+ \sqrt{2\alpha} {\epsilon}_t$$

这里$\tilde x_0 = x + \epsilon$, $\epsilon \sim N(0,\sigma^2I)$, 训练过程中，没有额外加噪声

紧接着我们再思考，与像DenoiseAutoEncoder其对数据加完噪声之后在训练，为何不在训练过程中边加噪声边训练呢？

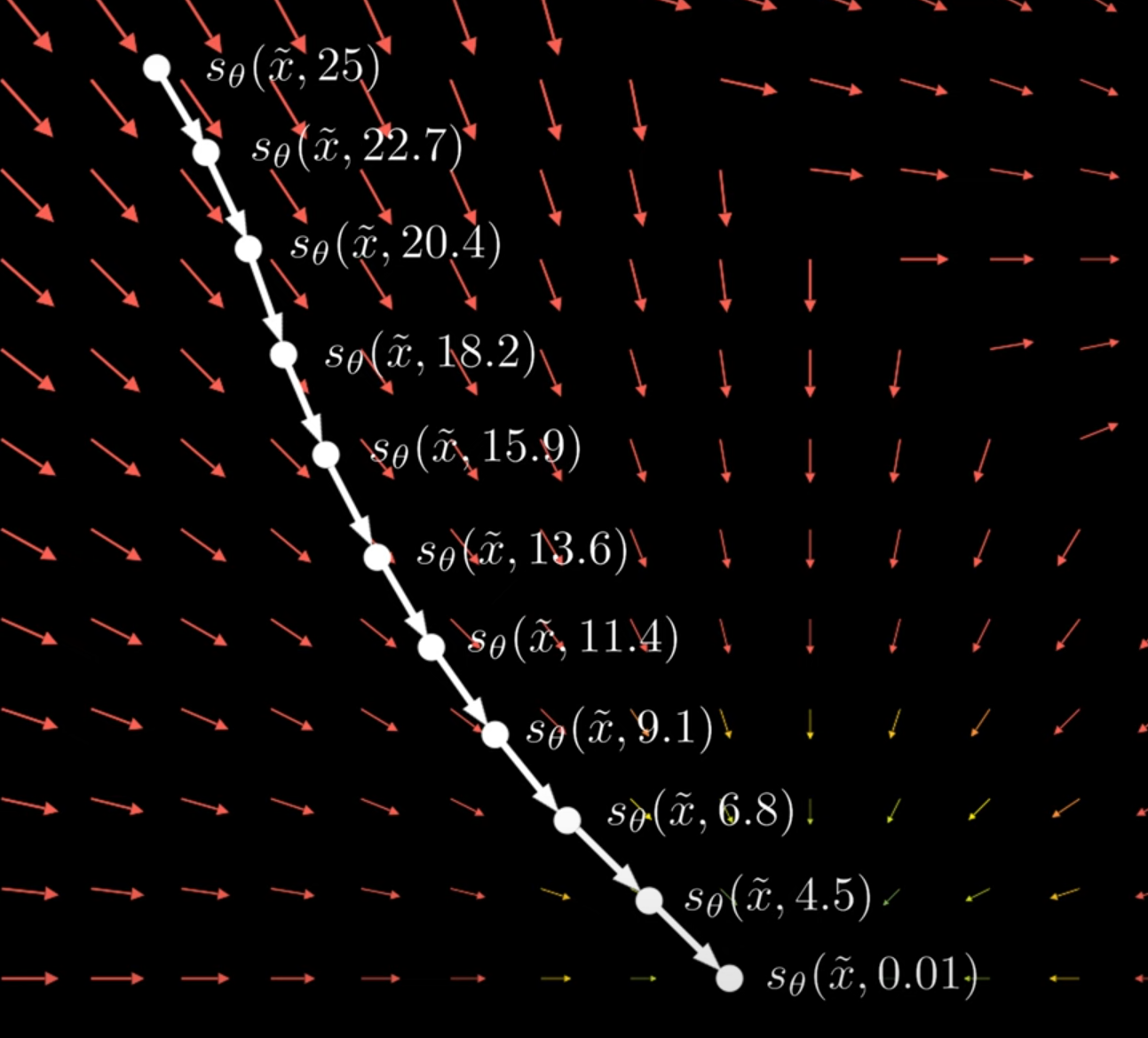
当噪声大时，模型能够见到更多的数据空间，增强鲁棒性/噪声小时，模型能够学到更精确的score

现在score model变为$s_{\theta}(\tilde x, \sigma_t)$

Score-Based Generative Modeling through Stochastic Differential Equations 指出，当添加的噪声级别到大无穷多的时候，演变为随机过程。

SDE

随机过程描述随时间或空间变化的随机现象的一类系统，它可以通过随机微分方程来描述

$$dx = f(x,t)dt + g(t)dw$$

• $f(x,t)$ 被称为漂移系数，表明系统确定性演化趋势
• $g(t)$ 被称为扩散系数， 表明随机噪声的强度
• $w$ 被称为维纳过程（Wiener Process，即布朗运动），是随机噪声的来源。 $dw∼N(0,dt)$

$\tilde x = x + \epsilon$, $\epsilon \sim N(0,\sigma_t^2I)$ 可以被表示为$dx = g(t)dw$, 没有漂移项，而$\sigma_t$对应就是时间$t$下的扩散系数$g(t)$

进一步的为了更好地和$g(t)$ 对齐，我们可以将$\sigma_t$写为关于$t$的函数$\sigma(t)$

统一表示形式:

模式	Forward SDE	Reverse SDE
通用	$\mathrm{d}x = f(x, t) \, \mathrm{d}t + g(t) \, \mathrm{d}w$	$\mathrm{d}x = \left[f(x, t) - g^2(t) \nabla_x \log p_\sigma(x)\right] \, \mathrm{d}t + g(t) \, \mathrm{d}w$
DDPM	$dx = \frac{1}{2}\beta_tdt + \sqrt\beta_tdw$	$dx = \frac{1}{\sqrt{1 - \beta_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_{\theta}(x_t, t) \right) + \sqrt{\beta_t} z$

SDE link to DDPM

$q(x_t|x_{t-1}) = \mathcal N(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_t I)$

$q(x_t|x_0) =\mathcal N(x_t; \sqrt{\bar \alpha_t}x_0, (1-\bar \alpha_t)I)$

Forward SDE

$x_t = \sqrt{1 - \beta_t} x_{t-1} + \sqrt\beta_t \epsilon$, $\epsilon \sim N(0,I)$

$x_t - x_{t-1}= \sqrt{1 - \beta_t} x_{t-1} + \sqrt\beta_t \epsilon - x_{t-1}$

$x_t - x_{t-1} = (1 - \frac{1}{2} \beta_t - 1)x_{t-1} + \sqrt\beta_t \epsilon$

$x_t - x_{t-1} = \frac{1}{2}\beta_t x_{t-1} + \sqrt\beta_t \epsilon$

推导出Forward SDE $dx = \frac{1}{2}\beta_tdt + \sqrt\beta_tdw$

Reverse SDE

离散时间步递推
$x_{t-1} = x_t + \frac{1}{2} \beta_t x_t + \beta_t \nabla_x \log p_{\sigma}(x_t) + \sqrt{\beta_t} z$

分数函数
$\nabla_x \log p_\sigma(x)=\nabla_x \log p_\sigma(x_t|x_0) = -\frac{\epsilon}{1-\bar \alpha_t} = -\frac{\epsilon_{\theta}(x_t,t)}{1-\bar \alpha_t}$
可得：
$x_{t-1} = \left(1 + \frac{1}{2} \beta_t\right) x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_{\theta}(x_t, t) + \sqrt{\beta_t} z$

利用近似关系$1 + \frac{1}{2} \beta_t \approx \frac{1}{\sqrt{1 - \beta_t}}$：
$x_{t-1} = \frac{1}{\sqrt{1 - \beta_t}} x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_{\theta}(x_t, t) + \sqrt{\beta_t} z$

DDPM Sampler

最终近似为DDPM中采样公式（具体见SCORE-BASED GENERATIVE MODELING中的Appendix E）：
$x_{t-1} = \frac{1}{\sqrt{1 - \beta_t}} \left( x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_{\theta}(x_t, t) \right) + \sqrt{\beta_t} z$