Parallel Processing
Baseline
矩阵乘法朴素实现
1 | |
当数组默认按行优先存储时
假设cache中的一个块能够装下数组的一行
朴素算法的miss次数约为:
- A矩阵每换一次行就要cache miss一次
- B矩阵k每加一次都要换
通过调整循环顺序,减少cache missing的次数
Method 1 loop reorder
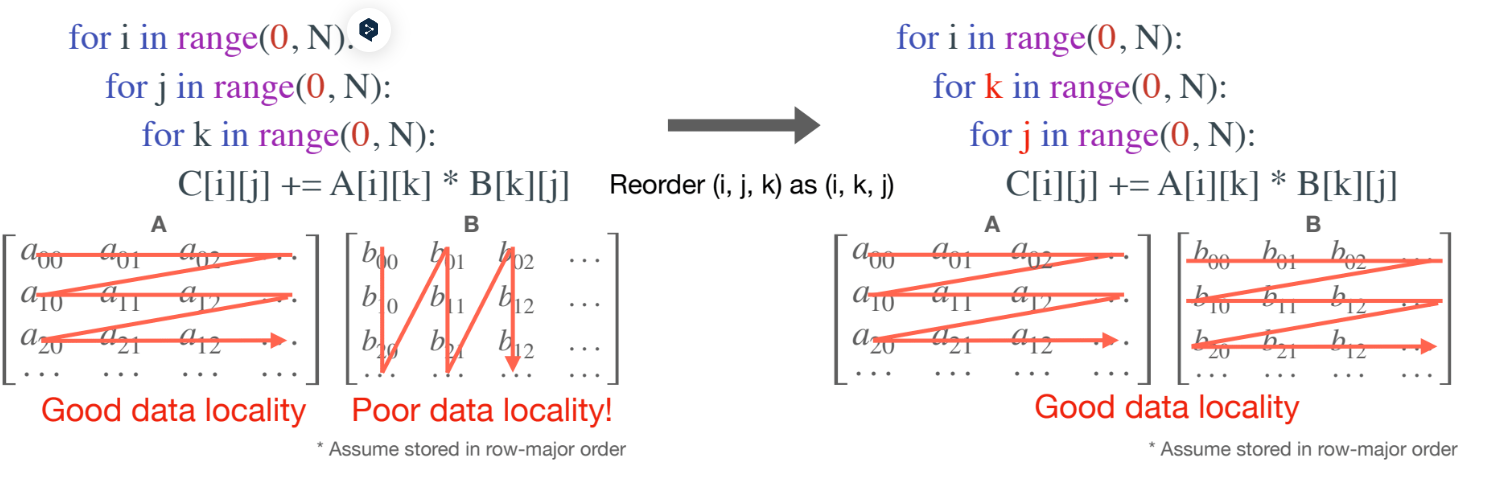
最简单的修改方式,优先以B的行来遍历。遍历顺序由ijk变为ikj
1 | |
miss次数:
Method 2 loop tilling
假设cache中的一个cache块一次不能装入一行怎么办?
那就装入能装的大小呗,不妨设置为TILE_SIZE
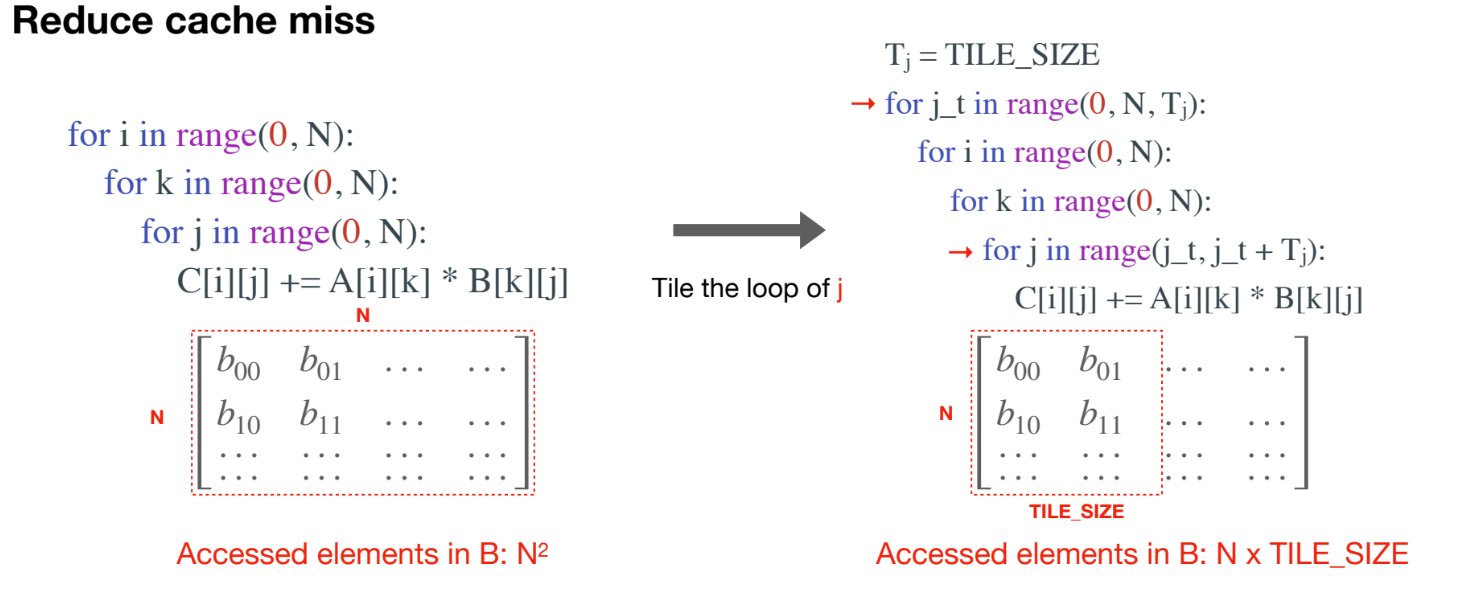
1 | |
上述只是考虑其中的一个cache块。
进一步地,如果整个cache缓存的大小,不足以装入矩阵的NxTILE_SIZE,我们一次就计算TILE_SIZExTILE_SIZE进一步减少cache miss的次数
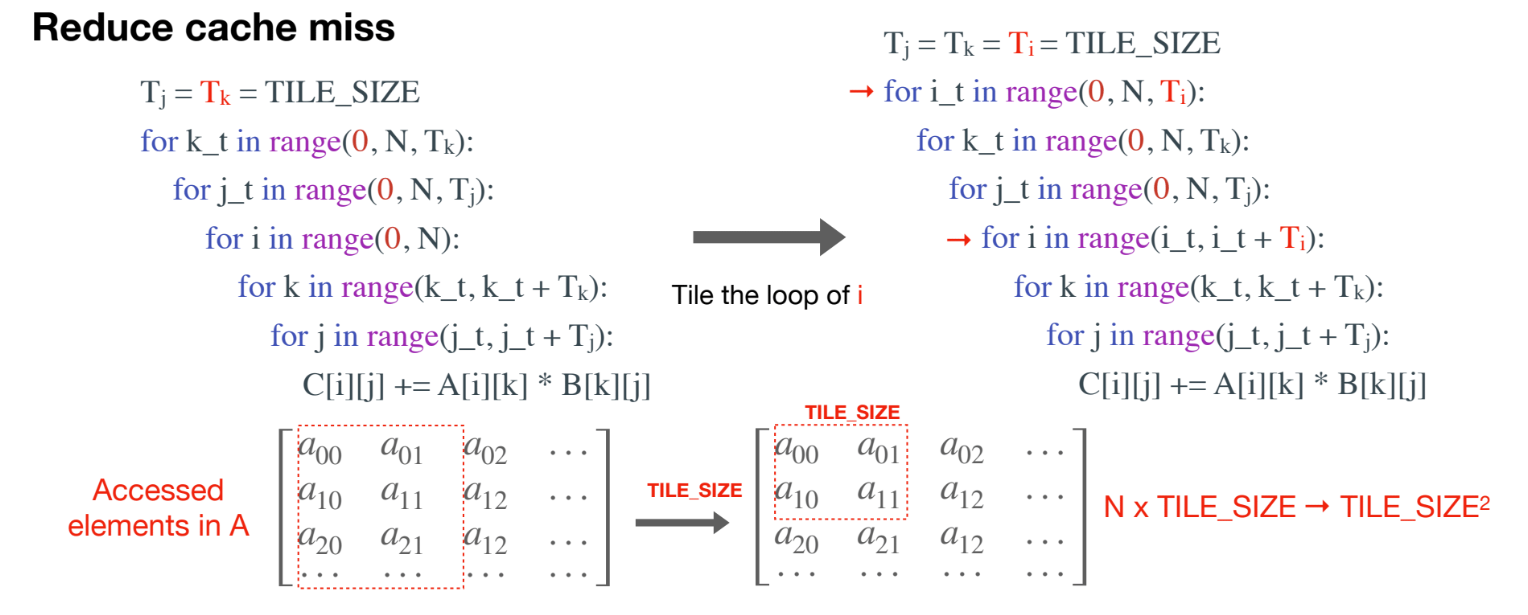
1 | |
Method 3 loop unrolling
通过循环展开,将循环体复制多次,从而减少循环迭代的次数。例如,原本循环迭代 100 次,展开后可能只迭代 25 次,每次迭代执行 4 次循环体的操作。
减少分支预测错误:由于循环次数减少,分支预测错误的机会也相应减少,从而提高了执行效率。
1 | |
Method 4 SISD programming
SISD意为一条指令执行多条数据
SSE(Streaming SIMD Extensions)是 Intel 提供的一种指令集扩展,用于加速多媒体和科学计算等任务。它通过 SIMD(Single Instruction, Multiple Data,单指令多数据)技术,允许一条指令同时处理多个数据,从而提高计算效率。
有以下三个接口:
_mm_load_ps / _mm_mul_ps / _mm_add_ps 解释
- _mm_load_ps
- 功能:加载 128 位(16 字节)的单精度浮点数(
float)到 SSE 寄存器。 - 解释:
_mm:表示这是 SSE 指令集的函数。load:表示加载数据。ps:表示 packed single-precision,即打包的单精度浮点数(float)。
- 示例:这会将
1
__m128 vec = _mm_load_ps(float* ptr);ptr指向的内存中的 4 个float值(共 128 位)加载到 SSE 寄存器vec中。
- _mm_mul_ps
- 功能:对两个 128 位的单精度浮点数向量进行逐元素相乘。
- 解释:
mul:表示乘法操作。ps:表示打包的单精度浮点数。
- 示例:这会将
1
__m128 result = _mm_mul_ps(vec1, vec2);vec1和vec2中的 4 个float值逐元素相乘,结果存储在result中。
- _mm_add_ps
- 功能:对两个 128 位的单精度浮点数向量进行逐元素相加。
- 解释:
add:表示加法操作。ps:表示打包的单精度浮点数。
- 示例:这会将
1
__m128 result = _mm_add_ps(vec1, vec2);vec1和vec2中的 4 个float值逐元素相加,结果存储在result中。
同样的AVX2指令集也有类似接口:
1 | |
llama2.c 使用Openmp + AVX加速矩阵乘法代码:
1 | |
Method 5 CUDA programming
Im2col Convolution
将卷积操作变为矩阵乘法
具体而言针对一个MxN的矩阵,和一个核大小为KxK的卷积核来讲,滑动窗口移动次数(M-K+1)(N-K+1)。每次固定滑动窗口后,都是卷积核和对应矩阵窗口进行逐元素对应乘积最后再求和。这个操作和一个行向量和列向量内积是等价的。
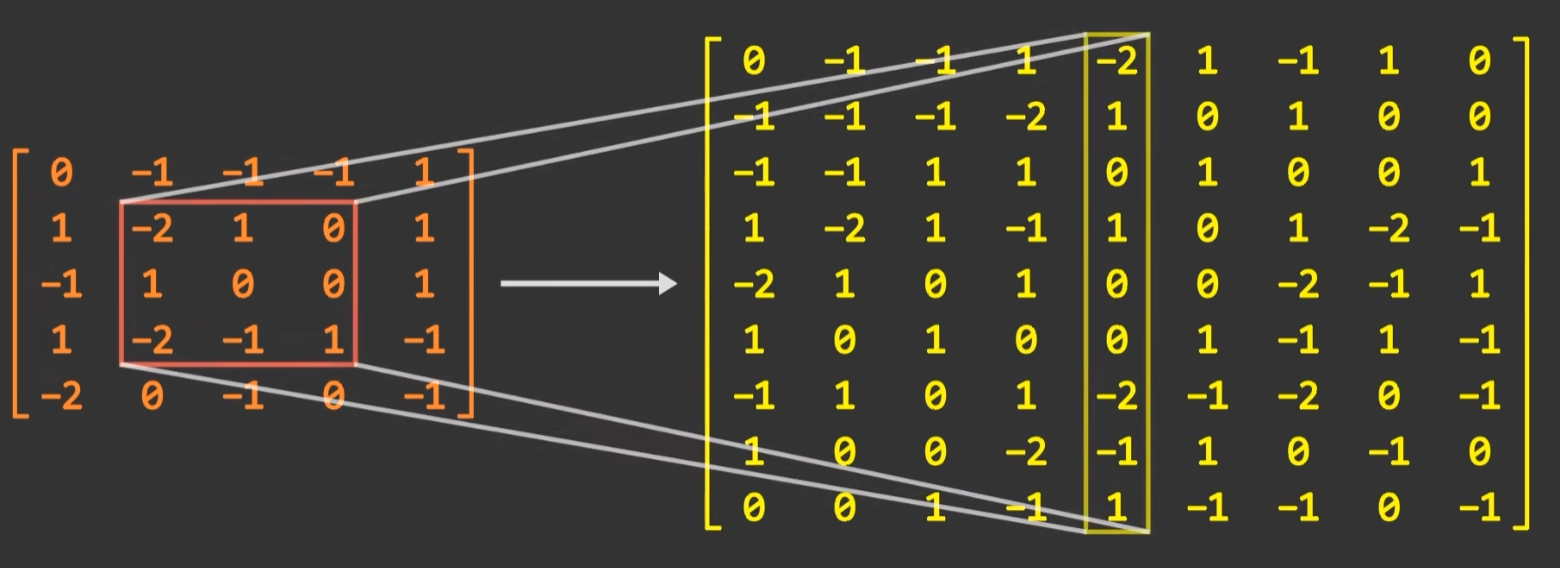
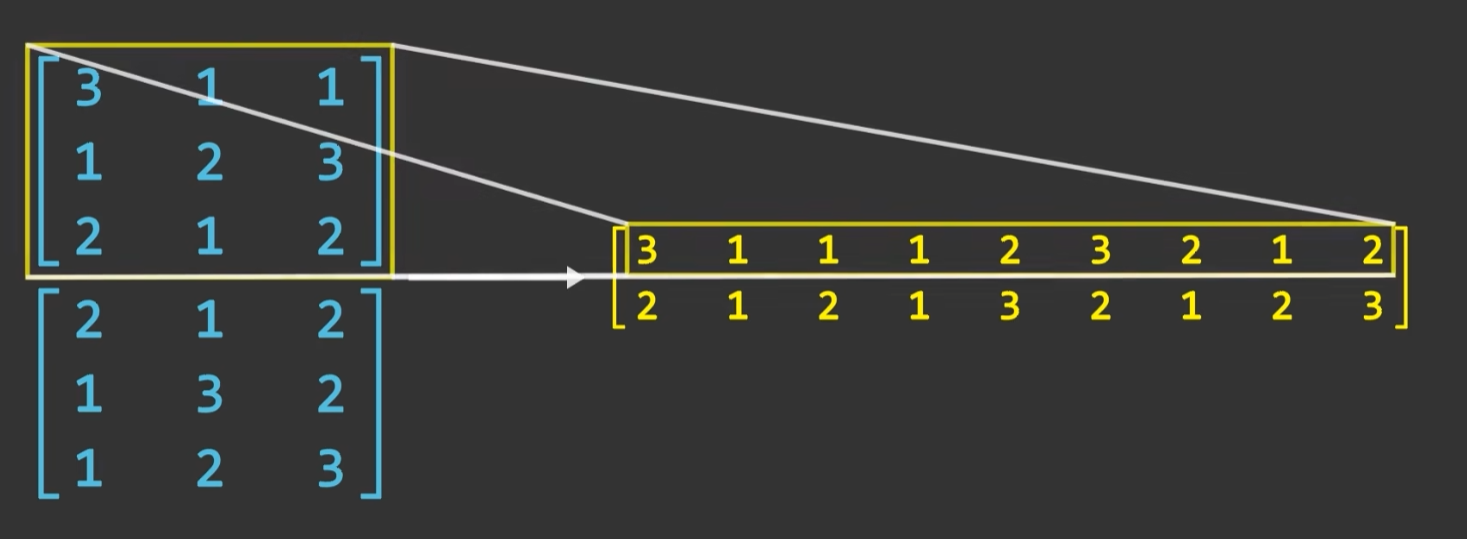
故我们可以将滑动窗口对应的矩阵窗口平铺为一个列向量,将卷积核平铺为一个行向量,二者内积便是单次计算结果。整个卷积操作等价于(M-K+1)(N-K+1)个列向量形成的矩阵以及对应卷积核形成矩阵的乘积
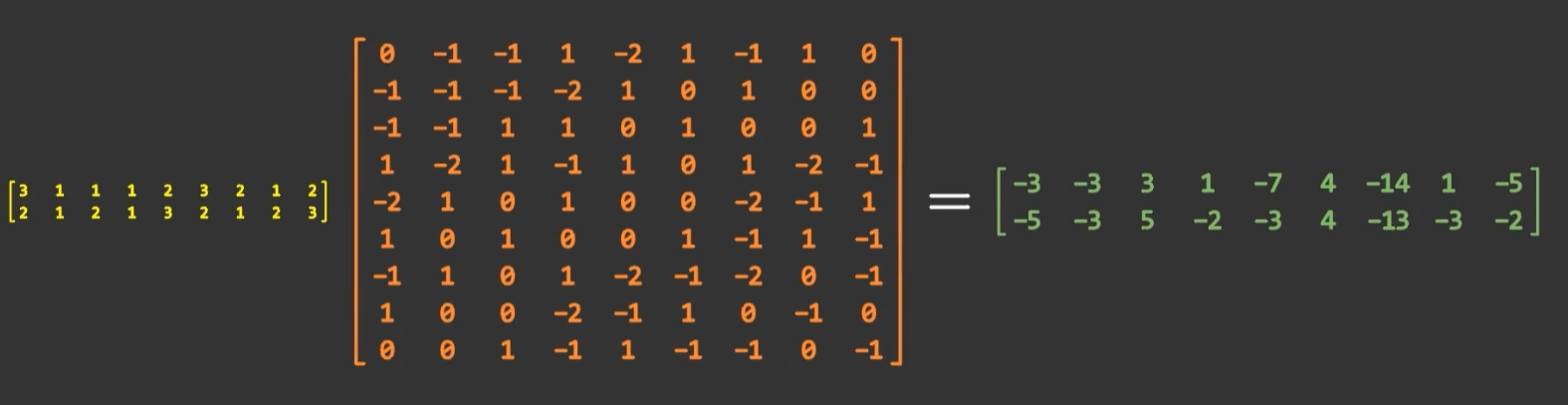
- 优点:可以使用矩阵乘法的高效算法
- 缺点:存储矩阵的内存开销增大,原来MxN,现在是(M-K+1)(N-K+1) x (KxK)
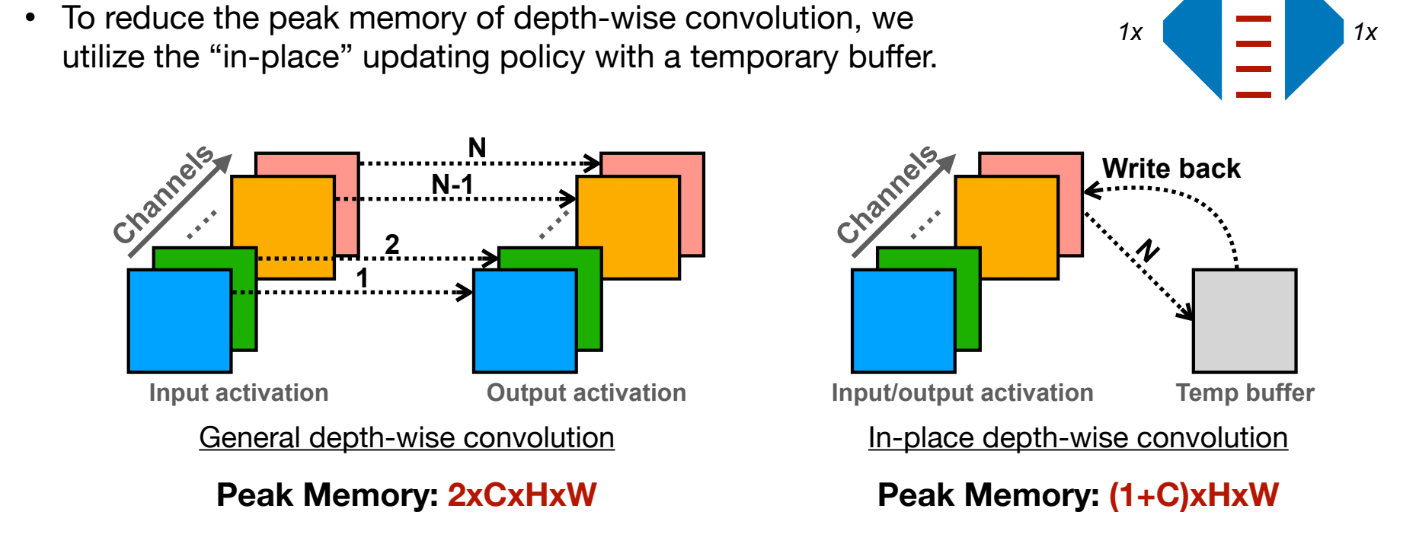
In-place Depth-wise Convolution
Peak Memory(峰值内存)问题
在普通的 Depth-wise Convolution 操作中:
每次卷积会产生一个新的输出张量。这个新的输出张量需要额外的内存来存储,导致模型运行时的峰值内存需求较高,尤其是对于高分辨率输入或多层网络时会放大问题。
In-place 策略的核心是直接在现有的内存块(如输入张量)上进行更新,而不额外分配新的内存块。对于计算的中间结果使用一个缓存区buffer保存
Winograd Convolution
一种加速卷积操作的数学算法(建立在乘法操作慢于加法操作的前提假设上)
- 推导不必掌握,只需知道公式即可
Others
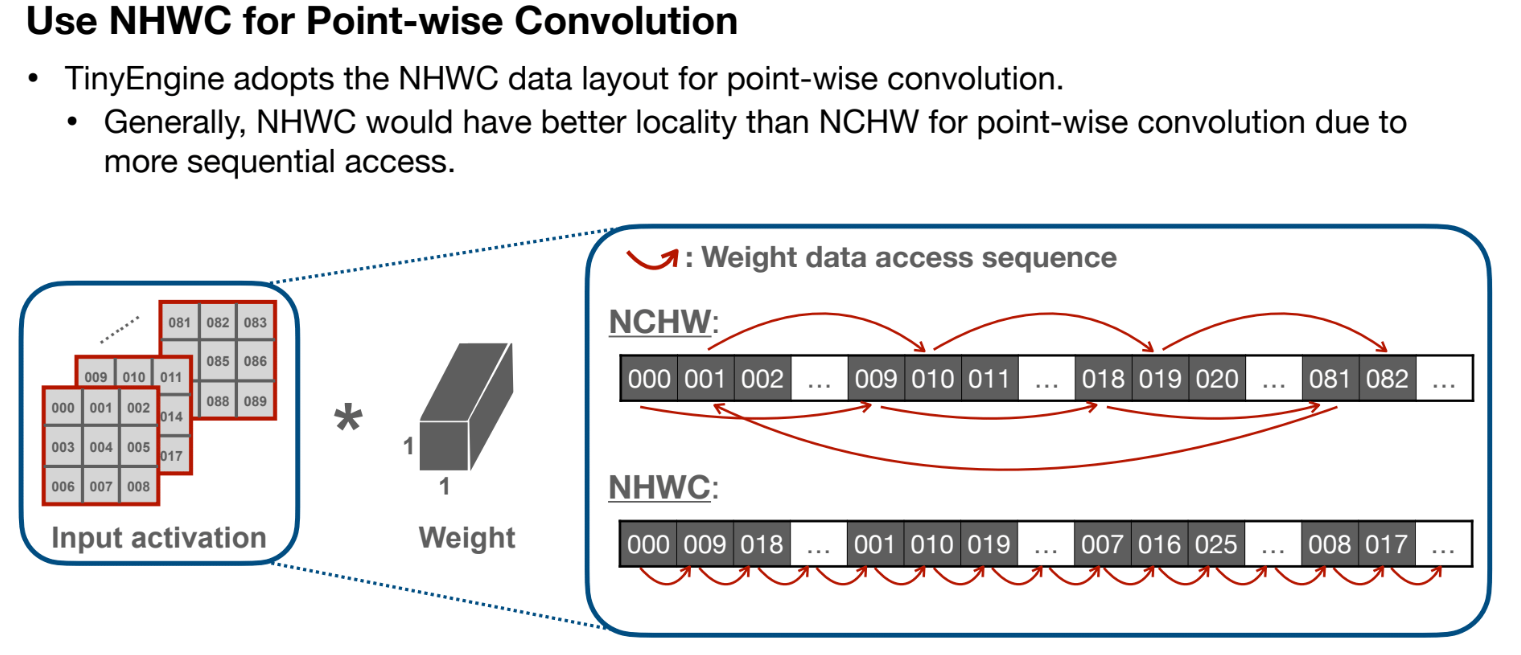
point-wise Convolution
- 单个卷积核为1x1xC,且对所有通道都要作用
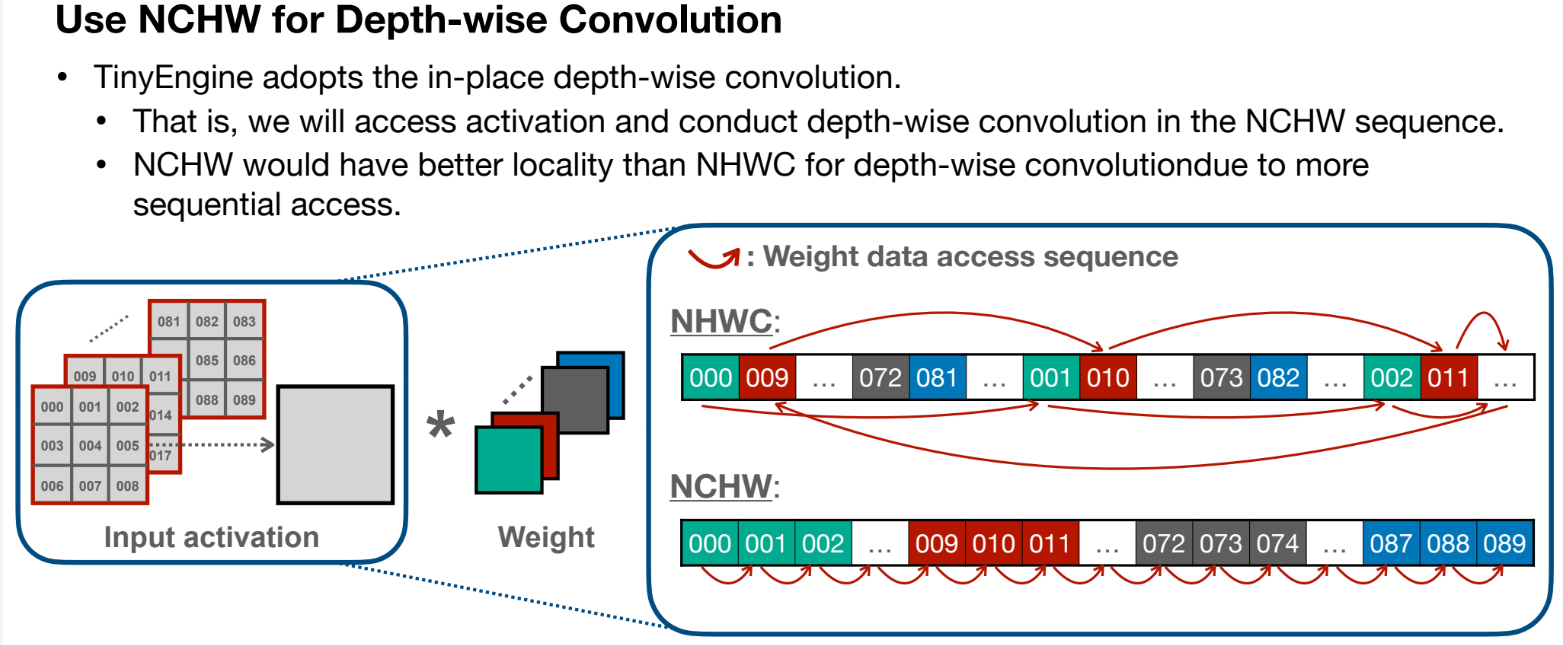
- 使用NHWC的格式存储输入矩阵,保证访问的连续性。
depth-wise Convolution
- 单个卷积核大小为KxKx1,只对一个通道作用,不同通道之间独立且使用不同卷积核处理
- 使用NCHW格式存储输入矩阵,保证访问的连续性。