RL1 MDP

基础概念

1. State: agent代理与环境交互时的状态

   1. state space：$S=\{s_{i}\}_{i=1}^n$ 即所有状态组成的集合

2. Action：$a_{i}$ 给定一个状态下所能采取的行动

   1. Action space of a state:$A(s_i) = \{a_j\}_{j=1}^m$ 给定一个状态下所能采取的所有行动组成的集合

3. State Transition：形如 $s_1 \xrightarrow{a} s_2$，在状态$s_1$ 采取行动$a$ 转移到状态 $s_2$

4. State transition probability: 状态转移概率，在一个状态采取行动a转移后的状态可能是不确定的

   1. 离散的（确定的情况）：

      $$\left\{ \begin{array}{l} p(s_2|s_1,a) = 1 \\ p(s_i|s_1,a) = 0 \space \forall i\neq 2 \end{array} \right.$$

   2. 随机的（符合一定的概率分布）

5. Policy: 描述在一个状态所能采取的行动分布

   

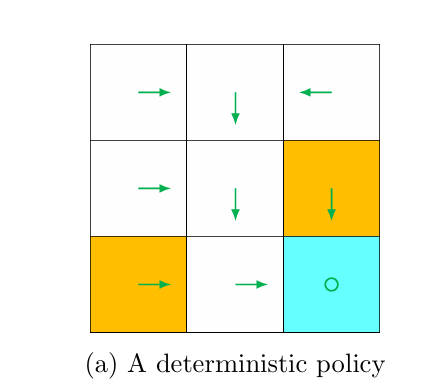
6. Reward:在状态采取行动会获得一定的奖励，注意奖励只跟当前状态和采取的行动有关，和下一刻转移到的状态无关。十分易错。与上方的状态转移概率相同，奖励也是服从一定分布的

   $p(r = 1|s_1,a_1) = 1$ and $p(r\neq 1|s_1,a_1)=0$

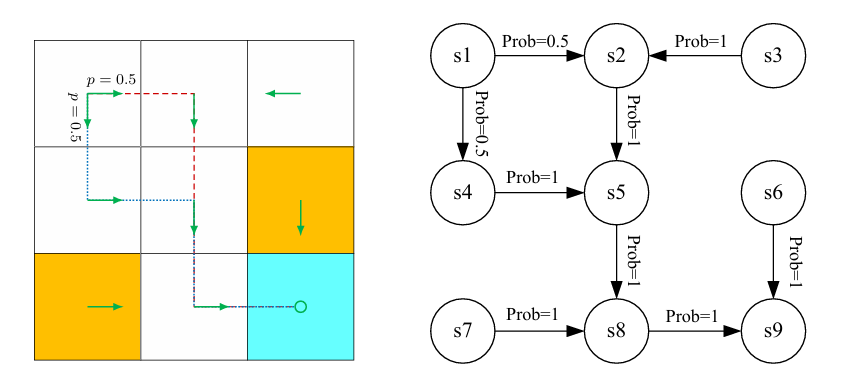
7. Trajectory : a state-action-reward chain

$$\begin{array}{ccccccc} S_{1} & \xrightarrow[r=0]{a_{3}} & S_{4} & \xrightarrow[r=-1]{a_{3}} & S_{7} & \xrightarrow[r=0]{a_{2}} & S_{8} & \xrightarrow[r=+1]{a_{2}} & S_{9} \end{array}$$

8. Return of a trajectory:将trajectory链上所获得奖励计算总和
   1. 然而trajectory可能是无限长的，因此通常会在计算return时增加折扣因子discount rate $\gamma \in [0,1]$， 折扣因子决定了智能体更关注短期奖励还是长期奖励
   2. $\gamma =0$：智能体只关心当前奖励，忽略未来奖励。
   3. $\gamma =1$：智能体平等对待当前和未来的所有奖励。
   4. $0 <\gamma <1$：智能体更重视近期奖励，同时也会考虑远期奖励（但远期奖励的权重会逐渐减小）。
9. 折扣回报公式：

$$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$$

10. Episode(or a trial): 智能体（Agent）在环境中按照某个策略（Policy）进行交互，直到到达某个终止状态（Terminal State）就停止的完整轨迹。
    • 由终止状态的任务称为 episodic tasks
    • 无终止状态的任务称为 continuing tasks

Markov decision process （MDP）

1. 集合（Sets）

• 状态（State）：状态集合 $S$。
• 动作（Action）：在状态 $s \in S$ 下，可用的动作集合 $A(s)$。
• 奖励（Reward）：在状态 $s$ 下采取动作 $a$ 后，可能获得的奖励集合 $R(s, a)$。

2. 概率分布（Probability Distributions）

• 状态转移概率（State Transition Probability）：

  • 在状态 $s$ 下采取动作 $a$，转移到状态 $s'$ 的概率为：

    $$p(s' \mid s, a)$$

• 奖励概率（Reward Probability）：

  • 在状态 $s$ 下采取动作 $a$，获得奖励 $r$ 的概率为：

    $$p(r \mid s, a)$$

3. 策略（Policy）

• 在状态 $s$ 下，选择动作 $a$ 的概率为：

  $$\pi(a \mid s)$$

4. 马尔可夫性质（Markov Property）

• 无记忆性（Memoryless Property）：

  • 下一个状态 $s_{t+1}$ 和奖励 $r_{t+1}$ 只依赖于当前状态 $s_t$ 和动作 $a_t$，而与之前的状态和动作无关。

  • 数学表示为：

    $$p(s_{t+1} \mid s_t, a_t, s_{t-1}, a_{t-1}, \dots, s_0, a_0) = p(s_{t+1} \mid s_t, a_t)$$

    $$p(r_{t+1} \mid s_t, a_t, s_{t-1}, a_{t-1}, \dots, s_0, a_0) = p(r_{t+1} \mid s_t, a_t)$$

5. MDP 框架

• 所有上述概念都可以放在 MDP 框架中：
  • 状态、动作、奖励 是 MDP 的基本组成部分。
  • 状态转移概率 和 奖励概率 定义了环境的动态特性。
  • 策略 是智能体的行为规则。
  • 马尔可夫性质 是 MDP 的核心假设，简化了问题的复杂性。