RL2 贝尔曼公式

回顾

折扣回报公式：

$$G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1}$$

可以帮助我们们衡量一个策略的好与坏，G更大的代表策略也更优。下面我们具体讲讲如何计算$G_t$

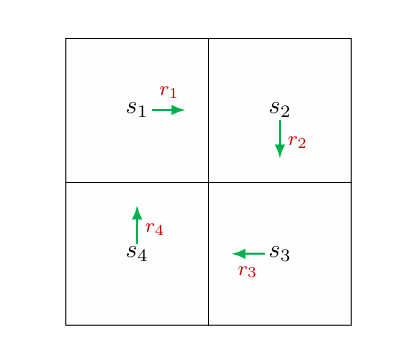
Method1：按照定义计算

$$\begin{align} v_1 &= r_1 + \gamma r_2 + \gamma ^{2}r_3 + ... \\ v_2 &= r_2 + \gamma r_3 + \gamma ^{2}r_4 + ... \\ v_3 &= r_3 + \gamma r_4 + \gamma ^{2}r_1 + ...\\ v_4 &= r_4 + \gamma r_1 + \gamma ^{2}r_2 + ... \end{align}$$

Method2：按照价值函数计算

$$\begin{align} v_1 &= r_1 + \gamma v_2 \\ v_2 &= r_2 + \gamma v_3 \\ v_3 &= r_3 + \gamma v_4 \\ v_4 &= r_4 + \gamma v_1 \end{align}$$

上述等式可以进一步写为矩阵的形式

$$\begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{bmatrix} = \begin{bmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \end{bmatrix} + \gamma \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{bmatrix}$$

对应的矩阵形式为：

$$\mathbf{V} = \mathbf{R} + \gamma \mathbf{P} \mathbf{V}$$

其中：

• $\mathbf{V} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{bmatrix}$：状态值函数的向量。
• $\mathbf{R} = \begin{bmatrix} r_1 \\ r_2 \\ r_3 \\ r_4 \end{bmatrix}$：即时奖励的向量。
• $\mathbf{P} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{bmatrix}$：状态转移概率矩阵。
• $\gamma$：折扣因子。

最终的解为：

$$\mathbf{V} = (\mathbf{I} - \gamma \mathbf{P})^{-1} \mathbf{R}$$

状态价值（State Value）

数学公式

状态值函数 $v_\pi(s)$ 定义为从状态 $s$ 开始，遵循策略 $\pi$ 的期望回报（Expected Return）：

$$v_\pi(s) = \mathbb{E}[G_t \mid S_t = s]$$

其中：

• $G_t$ 是从时间步 $t$ 开始的折扣回报（Discounted Return）。
• $S_t = s$ 表示当前状态为 $s$。
• $\mathbb{E}$ 表示期望值。

下面给出计算状态价值函数的推导

$$\begin{aligned} v_\pi(s) &= \mathbb{E}[G_t \mid S_t = s] \\ &= \mathbb{E}[R_t|S_t = S] + \gamma \mathbb{E}[G_{t+1}|S_t=s] \\ &= \pi(a|s)\sum_ap(r|s,a)r + \gamma \cdot\ \pi(a|s)\sum_{s^{'}}p(s^{'}|s,a)v_{\pi}(s^{'}) \\ &= \pi(a|s)[\sum_ap(r|s,a)r + \gamma \cdot \sum_{s^{'}}p(s^{'}|s,a)v_{\pi}(s^{'})]\\ &= r_{\pi}(s) + \gamma \sum _{s^{'}}p_{\pi}(s^{'}|s)v_{\pi}(s^{'}) \end{aligned}$$

写成矩阵形式：

$$v_{\pi} = r_{\pi} + \gamma P_{\pi}v_{\pi}$$

数值求解

$v_{\pi}$的closed-form(有限个标准数学运算)求解：

$$v_{\pi} = (I - \gamma P_{\pi})^{-1}r_{\pi}$$

实际上，我们通常采用迭代算法计算

$$v_{k+1} = r_{\pi} + \gamma P_{\pi}v_{k}$$

算法正确性证明：

定义误差为$\delta_k = v_k - v_{\pi}$。

我们只需要证明$\delta_k \to 0$。

将$v_{k+1} = \delta_{k+1} + v_{\pi}$和$v_k = \delta_k + v_{\pi}$代入方程$v_{k+1} = r_{\pi} + \gamma P_{\pi} v_k$，得到：

$$\delta_{k+1} + v_{\pi} = r_{\pi} + \gamma P_{\pi} (\delta_k + v_{\pi}),$$

可以改写为：

$$\delta_{k+1} = -v_{\pi} + r_{\pi} + \gamma P_{\pi} \delta_k + \gamma P_{\pi} v_{\pi}$$

$$= \gamma P_{\pi} \delta_k - v_{\pi} + (r_{\pi} + \gamma P_{\pi} v_{\pi})$$

$$= \gamma P_{\pi} \delta_k.$$

结果为：

$$\delta_{k+1} = \gamma P_{\pi} \delta_k = \gamma^2 P_{\pi}^2 \delta_{k-1} = \cdots = \gamma^{k+1} P_{\pi}^{k+1} \delta_0.$$

由于$P_{\pi}$的每个条目都不小于0且不大于1，我们有$0 \leq P_{\pi}^k \leq 1$，对于任何$k$都成立。

即$P_{\pi}^k$的每个条目都不大于1。另一方面，由于$\gamma < 1$，我们知道$\gamma^k \to 0$，因此$\delta_{k+1} = \gamma^{k+1} P_{\pi}^{k+1} \delta_0 \to 0$当$k \to \infty$时。

行动价值（Action Value)

$$q(s, a) = \mathbb{E}[G_t \mid S_t = s, A_t = a]$$

联系上述的状态价值公式

$$v_{\pi}(s) = \pi(a|s)\sum_a q(s,a)$$

不难得到行动价值公式

$$q(s,a) = \sum_ap(r|s,a)r + \gamma \cdot \sum_{s^{'}}p(s^{'}|s,a)v_{\pi}(s^{'})$$

• 状态价值：已知行动价值计算状态价值
• 行动价值：已知未来的状态价值计算当前的行动价值