RL4 从Model based 到 Model free的MC算法

回顾

上一讲中BOE解法实际上被称为值迭代算法（Value iteration algorithm）

值迭代算法（Value iteration algorithm）

该算法实际上就是两步：

  • 第一步 Policy update：

    πk+1(a∣s)={1当 a=ak∗(s)0当 a≠ak∗(s)\pi_{k+1}(a|s) = \begin{cases} 1 & \text{当 } a = a^*_k(s) \\ 0 & \text{当 } a \neq a^*_k(s) \end{cases}

  • 第二步 Value update:

    vk+1=rk+1+Pπk+1vk=qk(s,a)v_{k+1} = r_{k+1} + P_{\pi_{k+1}} v_{k} = q_k(s,a)

  • 注意迭代过程中每一步的vkv_k 实际上并不是贝尔曼公式中的状态价值，而是一个中间计算值，不具备物理含义

策略迭代算法 (Policy iteration algorithm)

该算法实际上也是两步：

  • 第一步 Policy evaluation:

    vk=rπk+γPπkvkv_{k} = r_{\pi_k} + \gamma P_{\pi_{k}} v_{k}

  • 第二步 Policy improvement:

    πk+1=argmaxπ(rπk+γPπkvk)\pi_{k+1} = argmax_{\pi}(r_{\pi_k} + \gamma P_{\pi_k}v_k)

  • 注意这里第一步是贝尔曼公式，这里的vkv_k不同于值迭代算法，是真正的状态价值。

  • 第一步的贝尔曼公式的求解相当于又嵌套了一层迭代循环

算法正确性证明：

首先证明：

If πk+1=argmaxπ(rπk+γPπkvπk)\pi_{k+1} = argmax_{\pi}(r_{\pi_k} + \gamma P_{\pi_k}v_{\pi_k} ), then vπk+1≥vπkv_{\pi_{k+1}} \ge v_{\pi_k}. Here, vπk+1≥vπkv_{\pi_{k+1}} \ge v_{\pi_k} means that vπk+1(s)≥vπk(s)v_{\pi_{k+1}}(s) \ge v_{\pi_k} (s) for all ss.

已知满足贝尔曼公式

vπk=rπk+γPπkvπkvπk+1=rπk+1+γPπk+1vπk+1v_{\pi_k} = r_{\pi_k} + \gamma P_{\pi_k}v_{\pi_k} \\v_{\pi_{k + 1}} = r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}}v_{\pi_{k+1}}

已知 πk+1=arg⁡max⁡π(rπk+γPπk+1vπk)\pi_{k+1} = \arg\max_{\pi} \left(r_{\pi_{k}} + \gamma P_{\pi_{k+1}} v_{\pi_k} \right),

所以rπk+1+γPπk+1vπk≥rπk+γPπkvπk\quad r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_k} \geq r_{\pi_k} + \gamma P_{\pi_k} v_{\pi_k}

故

vπk−vπk+1≤rπk+1+γPπk+1vπk−rπk+1+γPπk+1vπk+1≤γPπk+1(vπk−vπk+1)≤...≤γnPπk+1n(vπk−vπk+1)≤lim⁡n→∞γnPπk+1n(vπk−vπk+1)=0\begin{align*}v_{\pi_k} - v_{\pi_{k+1}} &\le r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_k} - r_{\pi_{k+1}} + \gamma P_{\pi_{k+1}} v_{\pi_{k+1}} \\&\le \gamma P_{\pi_{k+1}} (v_{\pi_k} - v_{\pi_{k+1}}) \le ... \le \gamma^{n}P^n_{\pi_{k+1}}(v_{\pi_k} - v_{\pi_{k+1}}) \\&\le \lim_{n \to \infty} \gamma^{n}P^n_{\pi_{k+1}}(v_{\pi_k} - v_{\pi_{k+1}}) = 0\end{align*}

极限的存在是因为 lim⁡n→∞γn=0\lim_{n \to \infty} \gamma^{n} = 0，并且对于任何 nn，Pπk+1nP_{\pi_{k+1}}^n​ 是一个非负的随机矩阵。

随机矩阵（stochastic matrix）是一种特殊类型的矩阵，它具有以下两个主要特征：

  1. 非负元素：矩阵中的每个元素都大于或等于零，即矩阵的元素不能是负数。
  2. 每行的元素之和为1：矩阵中每一行的所有元素的和等于1。这个特性保证了矩阵的每一行代表一个概率分布，因为概率的和必须为1。

因此 {vπ0,vπ1，...vπk}\{v_{\pi_0}, v_{\pi_1} ， ...v_{\pi_k}\}是一个单调递增的数列

又因为存在v∗≥vv^{*} \ge v 对于任意的vv， 根据单调递增数列必定收敛定理，上述算法最终一定收敛到v∗v^{*}

二者比较

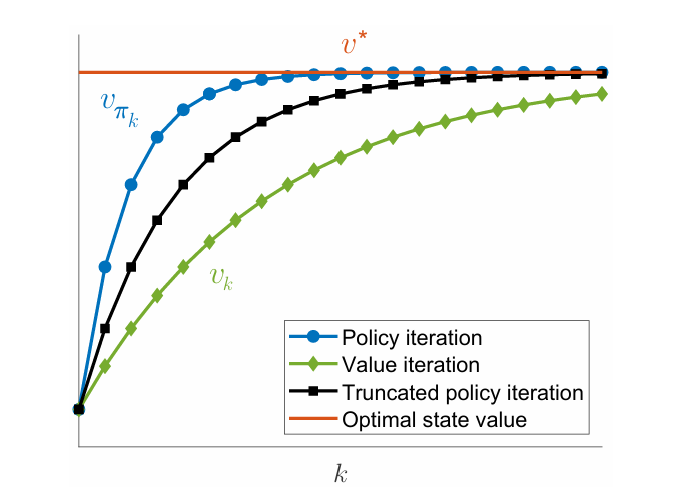
不难发现：值迭代算法上是策略迭代算法的退化版

  • 值迭代算法：在value update时只进行一步预测
  • 策略迭代算法：在value update时直到求解出真正的状态价值后才停止预测

Policy iteration:π0→PEvπ0→PIπ1→PEvπ1→PIπ2→PE⋯Value iteration:v0→PUπ1′→VUv1→PUπ2′→VUv2→PU⋯\begin{align*} \text{Policy iteration:} \quad & \pi_0 \xrightarrow{PE} v_{\pi_0} \xrightarrow{PI} \pi_1 \xrightarrow{PE} v_{\pi_1} \xrightarrow{PI} \pi_2 \xrightarrow{PE} \cdots \\ \text{Value iteration:} \quad & \hspace{1.3cm} v_0 \xrightarrow{PU} \pi_1' \xrightarrow{VU} v_1 \xrightarrow{PU} \pi_2' \xrightarrow{VU} v_2 \xrightarrow{PU} \cdots \end{align*}

故实际上存在二者中间的普适算法，称为中间跌断迭代算法Truncated policy iteration algorithm

即在value update时迭代jj步，jj为自定义超参数

MC Basic算法

上述算法都属于Model based算法，真实的概率分布均已知

Policy 算法需要已知 p(r∣s,a),p(s′∣s,a)p(r|s,a), p(s^{'}|s,a)，来求解出状态价值，之后再进行policy的优化

如果我们不能已知p(r∣s,a),p(s′∣s,a)p(r|s,a), p(s^{'}|s,a)的model，那该如何计算？

注意这里是不知道model具体的概率分布，但我们还是可以和model交互得到状态转移和奖励

这就属于Model free算法，即只有数据，而没有这些数据的真实分布。

蒙特卡罗（Monte Carlo）basic算法即利用大数定律，利用数据进行对动作状态价值做Mean estimation

已知当前的策略π\pi 后，选择每一对(s,a)(s,a)根据当前策略模拟大量episode (单个episode的长度理论上越长越好)，求return，最后计算平均，对动作状态价值进行更新，最后通过贪婪或者ϵ−greedy\epsilon - greedy 得到最优策略

qπk(s,a)=E[Gt∣St=s,At=a]≈1n∑i=1ngπk(i)(s,a).q_{\pi_k}(s, a) = \mathbb{E}[G_t | S_t = s, A_t = a] \approx \frac{1}{n} \sum_{i=1}^{n} g_{\pi_k}^{(i)}(s, a).

MC Exploring Starts算法

朴素的MC Basic算法很低效：

  1. 一个episode只用于一个(s,a)(s,a)的估计

考虑如下的一段episode:

s1→a2s2→a4s1→a2s2→a3s5→a1…\begin{equation} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_4} s_1 \xrightarrow{a_2} s_2 \xrightarrow{a_3} s_5 \xrightarrow{a_1} \ldots \tag{} \end{equation}

事实上可以为(s1,a2)(s_1, a_2), (s2,a4)(s_2, a_4), (s2,a3)(s_2, a_3) …多个对进行估计

其中有两种形式

  • every visit： 一条episode由前往后，对于每个(s,a)都用剩下的episode进行估计
  • first visit：一条episode由前往后，遇到之前未出现过的(s,a)都用剩下的episode进行估计
  1. 等收集到所有episode后才更新policy

可以类似梯度下降一样，收集到一个episode就更新一次

针对以上两点MC Exploring Starts对此做了优化

  • 其中exploring starts条件意为初始(s0,a0)(s_0, a_0)要保证所有状态动作对都可能被访问到

MC ϵ\epsilon-Greedy

MC Basic 和 Mc Exploring Starts都需要对(s,a)(s,a)有良好的估计和探索，然而使用确定的策略（即每个状态下只有一个可能的动作）对该估计有较大限制，MC ϵ\epsilon-Greedy采用soft policy来解决该问题

具体而言，基于MC Exploring Starts，MC ϵ\epsilon-Greedy将policy improvement中的完全贪心形式改为：

πk+1(a∣s)={1−∣A(s)∣−1∣A(s)∣ϵ,a=ak∗,1∣A(s)∣ϵ,a≠ak∗.\pi_{k+1}(a|s) = \begin{cases} 1 - \dfrac{|A(s)| - 1}{|A(s)|} \epsilon, & a = a_k^*, \\ \dfrac{1}{|A(s)|} \epsilon, & a \neq a_k^*. \end{cases}

  • 其中ϵ∈[0,1]\epsilon \in [0,1], ∣A(S)∣|A(S)| 是该状态下可能的所有动作的数量
  • 既保证行动价值最高的策略施行概率大(greedy)
  • 也保证了每个动作都可能被执行(explore)

算法流程：

一个重要的结论：

当ϵ\epsilon较小时，MC ϵ\epsilon-Greedy所得到的optimal ϵ\epsilon-Greedy Policy与最优的greedy Policy能够保持consistent，即ϵ\epsilon-Greedy Policy中概率最大的行动对应于greedy Policy中概率=1的行动（但当ϵ\epsilon如何较大，最终得到的策略可能不于最优策略保持一致）

  • 因此在实际部署时，我们还需要将ϵ\epsilon-Greedy Policy转化为greedy Policy来得到最优策略
#Reinforcement learning
RL4 从Model based 到 Model free的MC算法
https://xrlexpert.github.io/2025/02/12/RL4/
作者
Hirox
发布于
2025年2月12日
许可协议