RL7 值函数近似

值函数近似概念

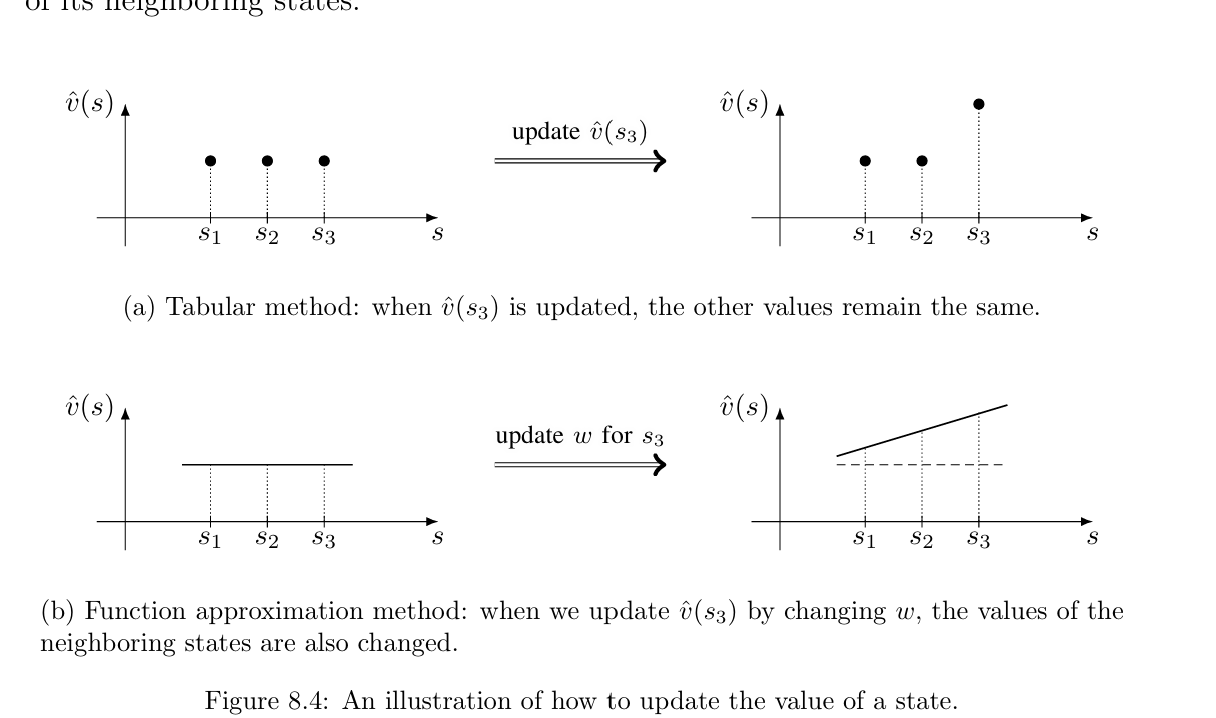
当状态$S$空间大或者是连续而非离散时，直接存储一个离散全量的值函数表 $v(s)$ 或 $q(s,a)$ 是不可行的，需要学习 一个可近似值函数的变量模型，进而用函数估计这些值。

一般将值函数近似表示为:

$$\hat{v}(s,\theta) \sim v_{\pi}(s)$$

其中：

• $\theta$ 是参数向量，$d$ 较小，遥异于状态数量
• $\hat{v}(s;\theta)$ 是由参数模型计算出来的近似值

因此，我们的目标是让 $\hat{v}(s;\theta)$ 尽可能接近 $v_\pi(s)$，通过学习最优化参数 $\theta$ 进行调整。

损失函数

定义相关的损失函数：

$$J(\theta) = \mathbb{E}_\pi[(v_\pi(S) - \hat{v}(S; \theta))^2]$$

即，在给定策略下，尽可能减少近似误差。

然而对于该期望，我们需要确定状态$S$的分布，常见的两种选择：

• 平均分布（Uniform Distribution）：平等看待所有状态，乘以 $1/|S|$ 。但这样并不好，因为显然不同状态的重要程度不一样
• 稳态分布（Stationary Distribution）：用于描述长期行为（long-run behavior），将一个智能体长期放置在环境中，以策略 π 进行交互，最终可以统计出智能体在每个状态停留的概率 ${d_{\pi}(s)},s∈S$

如果我们知道状态转移的概率矩阵 $P \in R^{n \times n}$， $P_{ij}$表示从状态$i$直接转移到状态$j$的概率， 那么我们可以直接计算出$d_{\pi}(s), s\in S$

利用下列条件，待定系数求解：

$$d_{\pi}(s)^T = d_{\pi}(s)^TP$$

此时上述的期望转变为

$$\begin{align} J(\theta) &= \mathbb{E}_\pi[(v_\pi(S) - \hat{v}(S; \theta))^2] \\ &= \sum_{s\in S} d_{\pi}(s)[v_{\pi}(s) - \hat{v}(s;\theta)]^2 \end{align}$$

对拟合函数参数更新使用随机梯度下降：

$$\begin{align} \theta_{t+1} &= \theta_t - \alpha_t \Delta J_{\theta} \\ &= w_t + 2\alpha_t(v_{\pi}(s_t) - \hat{v}(s_t;\theta_t))\nabla_{\theta}\hat{v}(s_t;\theta_t) \end{align}$$

TD learning

回忆朴素时序差分，直接将上述$v_{\pi}(s_t)$ 替换为 TD Target 即可

$$\theta_{t+1}= \theta_t + 2\alpha_t[r_{t+1} + \hat{v}(s_{t+1}, \theta_t)- \hat{v}(s_t;\theta_t)]\nabla_{\theta}\hat{v}(s_t;\theta_t)$$

在上面这些内容里，我们只讨论了 状态价值函数 v(s)的近似 。
但如果目标是 直接找出最优策略 $\pi(s)$，光有$v(s)$ 还不够——我们必须估计 最优动作价值函数 $q(s,a)$，因为策略的贪婪决策规则就是

$\pi(s) = \max_{a}q(s,a)$

于是下一步就是把 动作价值函数近似 搬到实践中，而常用的两条路径正好对应于经典的Sara和Q-learning

Sara

将原本的$q(s_t, a_t)$替换为神经网络即可

Q-learning

如果函数架构采用深度网络也就是著名的 Deep Q-Network(DQN)

将Q-learning中的状态价值函数替换为神经网络来预测即可

$$\theta_{t+1}= \theta_t + \alpha_t[r_{t+1} + \gamma \max_{a\in A(s_{t+1})}\hat{q}(s_{t+1}, a, \theta_{t})- \hat{q}(s_{t}, a_t, \theta_{t})]\nabla_{\theta}\hat{q}(s_{t}, a_t, \theta_{t})$$

然而对于更新项 $y=r_{t+1} + \gamma \max_{a\in A(s_{t+1})}\hat{q}(s_{t+1}, a, \theta_{t})$ ，有个max项不好求梯度。

在实际更新时，通常采用双网络形式。

• Target 神经网络冻结参数作为$y$的预测
• Main 神经网路用于计算 $\hat{q}(s_{t}, a_t, \theta_{t})$ 且参数可更新。每经历一定的步数，就将Main神经网络参数复制给Target神经网络。
• Target 可以看作Main的一个 延迟副本

另外，作为训练数据的经验$(s_t, a_t, s_{t+1}, r_{t+1})$ 需要放在一个buffer中，每次从中均匀采样出一个minibatch来训练而不是按照时间顺序来使用，这也被称为 经验回放

优点:

• 采用均匀采样

  在理论上假设随机变量 (S,A) 均匀分布 → 目标函数 $J(\theta) = \mathbb{E}_\pi[(v_\pi(S) - \hat{v}(S; \theta))^2]$ 有意义。若按收集顺序使用，样本分布跟行为策略耦合且相关；随机均匀抽样能最好地逼近独立同分布假设。

• 提高样本效率：每条经验可被反复利用多次，而非用完即弃。

off-policy: 生产数据的是另外一个网络，该方法只需最后一步利用最优的动作状态价值函数计算最优策略即可(加上DQN特有的双网络训练，实际参与的有三个网络)

on-policy: 生产数据和梯度更新的是一个网络，策略在每一步梯度更新时都需要重新计算